题目内容
已知铁矿石A和B的含铁率为a,冶炼每万吨铁矿石的排放量为b,及每万吨铁矿石的价格c,如表:
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为 (百万元).
【答案】分析:由已知条件中,铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2排放量b及每万吨铁矿石的价格c,对应的表格,再根据生产量不少于 1.9(万吨)铁,及CO2的排放量不超过2(万吨)我们可以构造出约束条件,并画出可行域,利用角点法求出购买铁矿石的最少费用.
解答: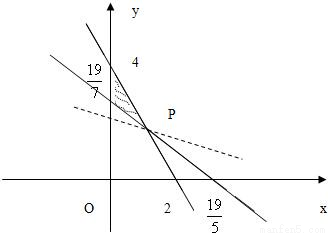 解:答案:15解析设铁矿石A购买了x万吨,铁矿石B购买了y万吨,购买铁矿石的费用为z百万元,则由题设知,本题即求实数x,y满足约束条件
解:答案:15解析设铁矿石A购买了x万吨,铁矿石B购买了y万吨,购买铁矿石的费用为z百万元,则由题设知,本题即求实数x,y满足约束条件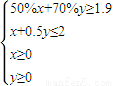 ,
,
即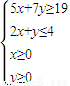 时,z=3x+6y的最小值.
时,z=3x+6y的最小值.
作不等式组对应的平面区域,如图阴影部分所示.
现让直线z=3x+6y,
即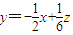 平移分析即知,
平移分析即知,
当直线经过点P时,z取得最小值.
又解方程组 得点P坐标为(1,2).
得点P坐标为(1,2).
故zmin=3×1+6×2=15.
故答案为:15.
点评:在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件⇒②由约束条件画出可行域⇒③分析目标函数Z与直线截距之间的关系⇒④使用平移直线法求出最优解⇒⑤还原到现实问题中.
解答:
 解:答案:15解析设铁矿石A购买了x万吨,铁矿石B购买了y万吨,购买铁矿石的费用为z百万元,则由题设知,本题即求实数x,y满足约束条件
解:答案:15解析设铁矿石A购买了x万吨,铁矿石B购买了y万吨,购买铁矿石的费用为z百万元,则由题设知,本题即求实数x,y满足约束条件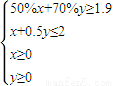 ,
,即
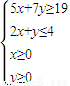 时,z=3x+6y的最小值.
时,z=3x+6y的最小值.作不等式组对应的平面区域,如图阴影部分所示.
现让直线z=3x+6y,
即
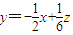 平移分析即知,
平移分析即知,当直线经过点P时,z取得最小值.
又解方程组
 得点P坐标为(1,2).
得点P坐标为(1,2).故zmin=3×1+6×2=15.
故答案为:15.
点评:在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件⇒②由约束条件画出可行域⇒③分析目标函数Z与直线截距之间的关系⇒④使用平移直线法求出最优解⇒⑤还原到现实问题中.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
