题目内容
如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.

【答案】
当休闲广场的长为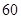 米,宽为
米,宽为 米时,绿化区域总面积最大值,最大面积为
米时,绿化区域总面积最大值,最大面积为 平方米.
平方米.
【解析】
试题分析:先将休闲广场的长度设为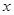 米,并将宽度也用
米,并将宽度也用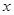 进行表示,并将绿化区域的面积
进行表示,并将绿化区域的面积 表示成
表示成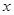 的函数表达式,利用基本不等式来求出绿化区域面积的最大值,但是要注意基本不等式适用的三个条件.
的函数表达式,利用基本不等式来求出绿化区域面积的最大值,但是要注意基本不等式适用的三个条件.
试题解析:设休闲广场的长为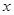 米,则宽为
米,则宽为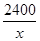 米,绿化区域的总面积为
米,绿化区域的总面积为 平方米,
平方米,
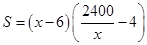 6分
6分

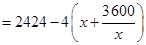 ,
,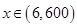 8分
8分
因为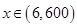 ,所以
,所以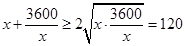 ,
,
当且仅当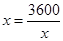 ,即
,即 时取等号
12分
时取等号
12分
此时 取得最大值,最大值为
取得最大值,最大值为 .
.
答:当休闲广场的长为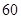 米,宽为
米,宽为 米时,绿化区域总面积最大值,最大面积为
米时,绿化区域总面积最大值,最大面积为 平方米.
平方米.
14分
考点:矩形的面积、基本不等式

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.
如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米. 如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.
如图,某小区拟在空地上建一个占地面积为2400平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为2米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.