题目内容
在棱长为1的正四面体A1A2A3A4中,记aij=|
•
| (i,j=1,2,3,4, i≠j),则aij不同取值的个数为( )
| A1A2 |
| AiAj |
| A、6 | B、5 | C、3 | D、2 |
分析:根据正四面体A1A2A3A4的结构特征,我们易分析出正四面体A1A2A3A4中,所有棱与棱A1A2的位置关系,再根据aij=|
•
| (i,j=1,2,3,4, i≠j),我们易得到aij不同取值的个数.
| A1A2 |
| AiAj |
解答:解:在正四面体A1A2A3A4中,
所有棱与棱A1A2的关系可分为三类:
①棱A1A2本身;②与棱A1A2相交,其夹角为60°;③与棱A1A2异面,其夹角为90°
故当aij=|
•
| (i,j=1,2,3,4, i≠j)时,
aij的值可能为:1(对应情况①);
(对应情况②);0(对应情况③).
故选C
所有棱与棱A1A2的关系可分为三类:
①棱A1A2本身;②与棱A1A2相交,其夹角为60°;③与棱A1A2异面,其夹角为90°
故当aij=|
| A1A2 |
| AiAj |
aij的值可能为:1(对应情况①);
| 1 |
| 2 |
故选C
点评:本题考查的知识点是棱锥的结构特征,其中根据棱锥的结构特征分析出正四面体A1A2A3A4中,所有棱与棱A1A2的位置关系,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
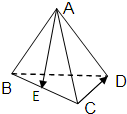 在棱长为1的正四面体ABCD中,E是BC的中点,则
在棱长为1的正四面体ABCD中,E是BC的中点,则 ( )
( ) C、
C、 D、
D、 www..com
高#考#资#源#
www..com
高#考#资#源#