Question

已知空间四边形OABC各边及其对角线OB、AC的长都是2，M、N分别是对边OA、BC的中点，点G是线段MN的中点，连结OG，则OG的长为

6

2

．

Answer 1

分析：根据题意，连结AN、ON，在正△ABC中算出AN=

3

，同理ON=

3

，从而算出MN=

ON2-OM2

=

2

，最后在△OMN中，利用中线的性质即可算出OG的长．

解答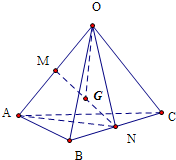：解：连结AN、ON
∵正△ABC的边长为2，∴AN=

3

2

AB=

3

，
同理得到ON=

3

∴等腰△OAN中，MN=

ON2-OM2

=

2

△OMN中，OG是中线
∴4OG²+MN²=2（OM²+ON²），
即4OG²+2=2[1²+（

3

）²]，解之得OG=

6

2

故答案为：

6

2

点评：本题在所有棱长均为2的四面体中求线段0G的长，着重考查了正三角形的性质、勾股定理和三角形中线的性质等知识，属于中档题．