题目内容
三棱锥中,四根棱长为a,其余两根棱长分别为| 2 |
| 3 |
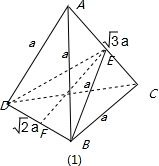
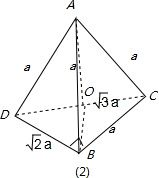
分析:画出图形,图(1)中找出垂面如图,判断是否存在,存在可求,垂面BDE面积,再求体积;图(2)中作出棱锥的高AO,求出底面BCD面积,高AO的长度,求出三棱锥的体积.
解答:解:由题意画出三棱锥的图形如图:
在图(1)中,过
a的直线作平面垂直
a的直线的平面如图,
EB=
a,EF=
,联B,D中点AF,CF,则AF+CF<AC,故此种情况不存在.
图(2)中取DC的中点O,易得AO⊥平面BCD,
所以底面面积为:
a2
高AO=
a棱锥的体积为:
×
a2×
a=
a3
故答案为:
在图(1)中,过
| 2 |
| 3 |
EB=
| 1 |
| 2 |
| ||
| 2 |
图(2)中取DC的中点O,易得AO⊥平面BCD,
所以底面面积为:
| ||
| 2 |
高AO=
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 12 |
故答案为:
| ||
| 12 |


点评:本题考查棱锥的体积的求法,作图能力,空间想象能力,分类讨论思想,是中档题.对棱锥的体积的求法,垂面法,高线法,是基本方法,值得同学学习.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
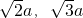 ,则这个三棱锥的体积是________a3.
,则这个三棱锥的体积是________a3.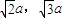 ,则这个三棱锥的体积是 a3.
,则这个三棱锥的体积是 a3.