题目内容
已知圆M的圆心M在x轴上,半径为1,直线l:y=![]() x-
x-![]() 被圆M所截的弦长为
被圆M所截的弦长为![]() ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.
(1)求圆M的方程;
(2)设A(0,t),B(0,t+6)(-5≤t≤-2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值和最小值.
(1)设圆心M(a,0),由已知得M到l:8x-6y-3=0的距离为![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
又∵M在l的下方,∴8a-3>0,∴8a-3=5,a=1.
故圆的方程为(x-1)2+y2=![]() 1.
1.
(2)由题设AC的斜率为k1,BC的斜率为k2,则直线AC的方程为y=k1x+t,直线BC的方程为y=k2x+t+6.
由方程组![]() ,得C点的横坐标为xc=
,得C点的横坐标为xc=![]() .
.
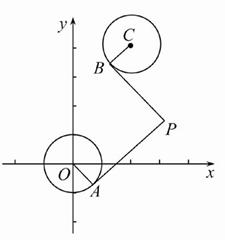 ∵|AB|=t+6-t=6,
∵|AB|=t+6-t=6,
∴S=![]() |
|![]() |·6=
|·6=![]() ,
,
由于圆M与AC相切,所以1=![]() ,∴k1=
,∴k1=![]() ;
;
同理,k2=![]() ,
,
∴k1-k2=![]() ,
,
∴S=![]() =6(1-
=6(1-![]() ),∵-5≤t≤-2.
),∵-5≤t≤-2.
∴-2≤t+3≤1,∴-8≤t2+6t+1≤-4,
∴Smax=6×(1+![]() )=
)=![]() ,Smin=6×(1+
,Smin=6×(1+![]() )=
)=![]() ,
,
∴△ABC的面积S的最大值为![]() ,最小值为
,最小值为![]() .
.

练习册系列答案
相关题目
 被圆M所截的弦长为
被圆M所截的弦长为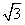 ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.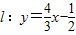 ,被圆M所截的弦长为
,被圆M所截的弦长为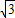 ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.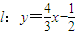 ,被圆M所截的弦长为
,被圆M所截的弦长为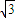 ,且圆心M在直线l的下方.
,且圆心M在直线l的下方.