题目内容
已知函数f(x)=![]() (x>0),设正项数列{an}的首项a1=2,前n项和Sn满足Sn=f(Sn-1)(n>1且n∈N*).
(x>0),设正项数列{an}的首项a1=2,前n项和Sn满足Sn=f(Sn-1)(n>1且n∈N*).
(1)求an的表达式.
(2)在平面直角坐标系内,直线Ln的斜率为an,且Ln与曲线y=x2有且仅有一个公共点,Ln又与y轴交于点Dn(0,bn),当n∈N*时,记dn=![]() .若
.若![]() ,求证:C1+C2+C3+…+Gn-n<1.
,求证:C1+C2+C3+…+Gn-n<1.
答案:
解析:
提示:
解析:
|
|
提示:
|
本题也可将C1+C2+C3+…+Cn-n化为 |

练习册系列答案
相关题目

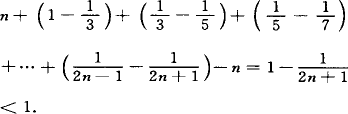
 ,通过研究{Cn-1}的通项入手解决.
,通过研究{Cn-1}的通项入手解决. )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有