题目内容
(1)求直线y=x+1被双曲线x2-
=1截得的弦长;
(2)求过定点(0,1)的直线被双曲线x2-
=1截得的弦中点轨迹方程.
| y2 |
| 4 |
(2)求过定点(0,1)的直线被双曲线x2-
| y2 |
| 4 |
分析:(1)直线y=x+1代入双曲线方程,利用韦达定理,即可求弦长;
(2)方法一:设直线的方程代入双曲线方程,利用韦达定理,可得关于k的表达式,消参,即可得到弦中点轨迹方程;
方法二:设弦的两个端点坐标,代入双曲线方程,利用点差法,即可求得结论.
(2)方法一:设直线的方程代入双曲线方程,利用韦达定理,可得关于k的表达式,消参,即可得到弦中点轨迹方程;
方法二:设弦的两个端点坐标,代入双曲线方程,利用点差法,即可求得结论.
解答:解:(1)由
得4x2-(x+1)2-4=0,即3x2-2x-5=0(*)
设方程(*)的解为x1,x2,则有x1+x2=
,x1x2=-
得,d=
|x1-x2|=
=
=
(2)方法一:若该直线的斜率不存在时与双曲线无交点,则设直线的方程为y=kx+1,它被双曲线截得的弦为AB对应的中点为P(x,y),
由
得(4-k2)x2-2kx-5=0(*)
设方程(*)的解为x1,x2,则△=4k2+20(4-k2)>0,
∴16k2<80,|k|<
,且x1+x2=
,x1x2=-
,
∴x=
(x1+x2)=
,y=
(y1+y2)=
(x1+x2)+1=
,
即
,消去k得4x2-y2+y=0(y<-4或y>0).
方法二:设弦的两个端点坐标为A(x1,y1),B(x2,y2),弦中点为P(x,y),则
,两式相减得:4(x1+x2)(x1-x2)=(y1+y2)(y1-y2),
∴
=
,即
=
,即4x2-y2+y=0(y<-4或y>0).
|
设方程(*)的解为x1,x2,则有x1+x2=
| 2 |
| 3 |
| 5 |
| 3 |
| 2 |
| 2 |
| (x1+x2)2-4x1x2 |
| 2 |
|
| 8 |
| 3 |
| 2 |
(2)方法一:若该直线的斜率不存在时与双曲线无交点,则设直线的方程为y=kx+1,它被双曲线截得的弦为AB对应的中点为P(x,y),
由
|
设方程(*)的解为x1,x2,则△=4k2+20(4-k2)>0,
∴16k2<80,|k|<
| 5 |
| 2k |
| 4-k2 |
| 5 |
| 4-k2 |
∴x=
| 1 |
| 2 |
| k |
| 4-k2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 4-k2 |
即
|
方法二:设弦的两个端点坐标为A(x1,y1),B(x2,y2),弦中点为P(x,y),则
|
∴
| y1+y2 |
| x1+x2 |
| 4(x1-x2) |
| y1-y2 |
| y |
| x |
| 4x |
| y-1 |
点评:本题考查直线与双曲线的位置关系,考查点差法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
 截得的弦长;
截得的弦长; 截得的弦中点轨迹方程.
截得的弦中点轨迹方程.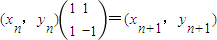 ,即
,即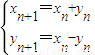 (n∈N*)为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换.我们把它称为点变换(或矩阵变换).已知P1(1,0).
(n∈N*)为点Pn(xn,yn)到点Pn+1(xn+1,yn+1)的一个变换.我们把它称为点变换(或矩阵变换).已知P1(1,0).