题目内容
(1)已知扇形OAB的圆心角α为120°,半径为6,求扇形弧长及所含弓形的面积.(2)已知扇形周长为
思路分析:将圆心角用弧度制表示后,利用弧长公式和扇形面积公式即可获解.对于(2),只需建立关于扇形面积S的函数,然后确定S最大时的条件.
解:(1)∵120°=![]() ,r=6,
,r=6,
∴l=![]() =
=![]() ·6=4π.
·6=4π.
∵S扇=![]() lr=
lr=![]() ·4π·6=12π,
·4π·6=12π,
S△OAB=![]() r2sin
r2sin![]() =
=![]() ×62×
×62×![]() =9
=9![]() ,
,
∴S弓形=S扇-S△OAB=12π-9![]() .
.
(2)设扇形的中心角为α,半径为r,弧长为l,
则由扇形的周长为20,得l=20-2r.
∴S扇=![]() lr=
lr=![]() (20-2r)r=10r-r2=-(r-5)2+25,
(20-2r)r=10r-r2=-(r-5)2+25,
其中由l>0,可推知0<r<10,
当r=5(cm)时面积S取最大值.
此时α=![]() =
=![]() =2弧度.
=2弧度.
答:(1)扇形弧长为4π,所含弓形面积为12π-9![]() 面积单位.(2)当扇形中心角为2弧度时,扇形面积最大,最大面积为
面积单位.(2)当扇形中心角为2弧度时,扇形面积最大,最大面积为

练习册系列答案
相关题目
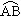 所对的圆心角是
所对的圆心角是 ,半径为50m,求
,半径为50m,求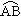 所对的圆心角是
所对的圆心角是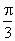 ,半径为50m,求
,半径为50m,求