题目内容
如图,在直角坐标系中,射线OA: x-y=0(x≥0),OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点.
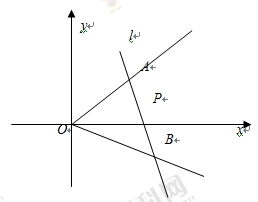
(1)当AB中点为P时,求直线AB的斜率
(2)当AB中点在直线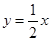 上时,求直线AB的方程.
上时,求直线AB的方程.

(1)当AB中点为P时,求直线AB的斜率
(2)当AB中点在直线
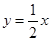 上时,求直线AB的方程.
上时,求直线AB的方程.(1) ;(2)
;(2)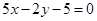
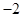 ;(2)
;(2)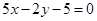
试题分析:(1)求直线的斜率有两种方法,一是求出倾斜角根据斜率定义
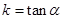 求斜率,二是求出直线上两点坐标,利用斜率公式
求斜率,二是求出直线上两点坐标,利用斜率公式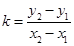 求斜率。本题属于第二种方法,应先设出A,B两点坐标,根据中点坐标公式求出A,B两点,再代入公式求斜率。(2)因为已知直线AB过点P,则可用点斜式求直线AB的方程,故可设其方程为
求斜率。本题属于第二种方法,应先设出A,B两点坐标,根据中点坐标公式求出A,B两点,再代入公式求斜率。(2)因为已知直线AB过点P,则可用点斜式求直线AB的方程,故可设其方程为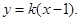 ,但需注意讨论斜率不存在时的情况。解两个方程组可求得点A,点B的坐标,利用中点坐标公式求出中点再代入
,但需注意讨论斜率不存在时的情况。解两个方程组可求得点A,点B的坐标,利用中点坐标公式求出中点再代入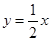 ,可解出K.
,可解出K.试题解析:解:(1)因为
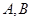 分别为直线与射线
分别为直线与射线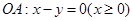 及
及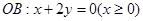 的交点,
的交点, 所以可设
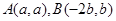 ,又点
,又点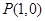 是
是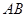 的中点,所以有
的中点,所以有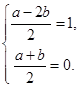 即
即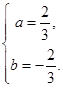
∴A、B两点的坐标为
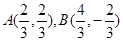 ,
,∴
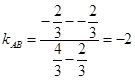 ,
,(2)①当直线
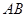 的斜率不存在时,则
的斜率不存在时,则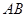 的方程为
的方程为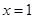 ,易知
,易知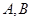 两点的坐标分别为
两点的坐标分别为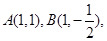 所以
所以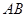 的中点坐标为
的中点坐标为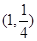 ,显然不在直线
,显然不在直线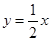 上,
上,即
 的斜率不存在时不满足条件.
的斜率不存在时不满足条件. ②当直线
 的斜率存在时,记为
的斜率存在时,记为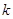 ,易知
,易知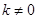 且
且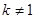 ,则直线
,则直线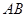 的方程为
的方程为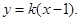
分别联立
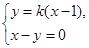 及
及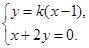
可求得
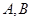 两点的坐标分别为
两点的坐标分别为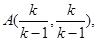
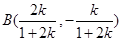
所以
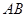 的中点坐标为
的中点坐标为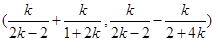 .
.又
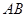 的中点在直线
的中点在直线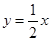 上,
上,所以
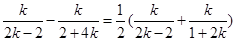 ,
,解之得
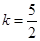 .
.所以直线
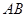 的方程为
的方程为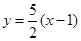 ,
,即
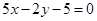 .
.
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 :
: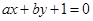 ,(
,(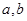 不同时为0),
不同时为0),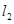 :
: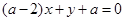 ,
,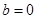 且
且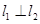 ,求实数
,求实数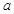 的值;
的值;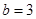 且
且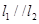 时,求直线
时,求直线 点射出,到
点射出,到 轴上的
轴上的 点后,被
点后,被 ,求
,求 所在直线的方程及点
所在直线的方程及点 和
和 互相垂直,则
互相垂直,则 等于( )
等于( )



 中,已知点
中,已知点 ,分别以
,分别以 的边
的边 向外作正方形
向外作正方形 与
与 ,则直线
,则直线 的一般式方程为 .
的一般式方程为 .
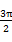 <α<2π,则直线
<α<2π,则直线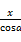 +
+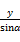 =1必不经过( )
=1必不经过( )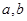 满足
满足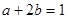 ,则直线
,则直线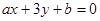 必过定点( )
必过定点( )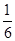 ,
,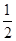 )
)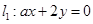 和
和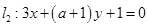 平行,则实数
平行,则实数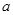 的值为 .
的值为 .