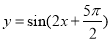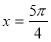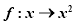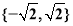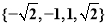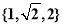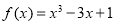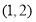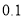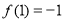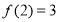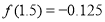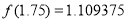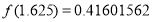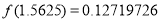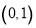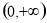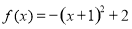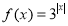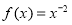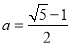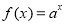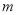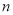题目内容
已知函数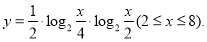
(Ⅰ)令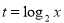 ,求
,求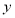 关于
关于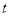 的函数关系式及
的函数关系式及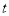 的取值范围;
的取值范围;
(Ⅱ)求函数的值域,并求函数取得最小值时的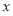 的值.
的值.
(Ⅰ)函数关系式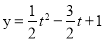 ,
,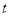 的取值范围
的取值范围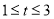
(Ⅱ)函数的值域为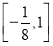 ,
,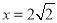 .
.
【解析】
试题分析:(Ⅰ)先利用对数的运算性质转化成关于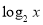 的函数
的函数 ,然后利用换元法转化为
,然后利用换元法转化为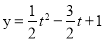 ,最后通过解不等式求出t的范围.
,最后通过解不等式求出t的范围.
(Ⅱ)利用数形结合的方法观察出值域,同时指明函数取得最小值时的 的值.本题最好的的方法就是数形结合,这样就比较直观的通过图像找出函数的最小值以及函数取得最小值时的
的值.本题最好的的方法就是数形结合,这样就比较直观的通过图像找出函数的最小值以及函数取得最小值时的 的值. 数形结合的方法是高考涉及到的重要的一种思想方法.
的值. 数形结合的方法是高考涉及到的重要的一种思想方法.
试题解析:(Ⅰ)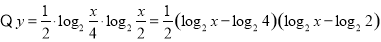
 .............2分
.............2分
令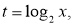 则
则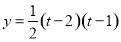 ,即
,即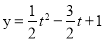 2分
2分
又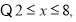
 ,即
,即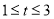
(Ⅱ)由(Ⅰ)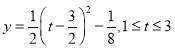 ,数形结合得
,数形结合得
当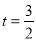 时,
时,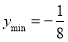 ,当
,当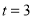 时,
时,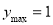 2分
2分
 函数的值域为
函数的值域为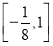 2分
2分
当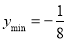 时,
时,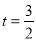 ,即
,即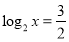 ,
,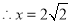 2分
2分
考点:1、对数的运算性质;2、数形结合的方法;3、二次函数求值域

练习册系列答案
相关题目