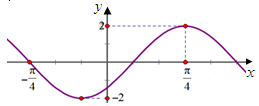
题目内容
点P在曲线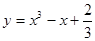 上移动,设在点P处的切线的倾斜角为为
上移动,设在点P处的切线的倾斜角为为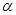 ,则
,则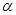 的取值范围是
的取值范围是
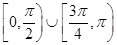
解析试题分析:根据导数的几何意义可知切线的斜率即为该点处的导数,再根据导数的取值范围求出斜率的范围,最后再根据斜率与倾斜角之间的关系k=tanα,求出α的范围即可。解:∵tanα=3x2-1,∴tanα∈[-1,+∞).=当tanα∈[0,+∞)时,α∈[0,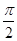 );当tanα∈[-1,0)时,α∈[,
);当tanα∈[-1,0)时,α∈[,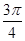 ,π).∴α∈[0,
,π).∴α∈[0,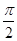 )∪[
)∪[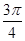 ,π).故答案
,π).故答案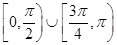 。
。
考点:导数研究曲线上某点切线的方程
点评:此题考查了利用导数研究曲线上某点切线的方程,直线倾斜角与斜率的关系,以及正切函数的图象与性质.要求学生掌握导函数在某点的函数值即为过这点切线方程的斜率,且直线的斜率为倾斜角的正切值,掌握正切函数的图象与性质.

练习册系列答案
相关题目
 )=
)=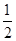 ,则sinθ+cosθ= .
,则sinθ+cosθ= .
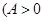 ,
,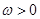 ,
,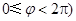 在
在 上的部分图象如图所示,则
上的部分图象如图所示,则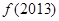 的值为 .
的值为 .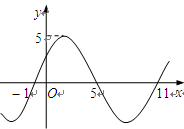
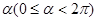 的终边过
的终边过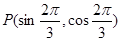 ,则
,则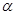 = .
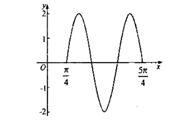
= .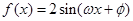 的图像如图所示,则
的图像如图所示,则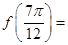 。
。
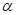 的终边过点
的终边过点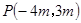 ,
, ,则
,则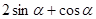 的值是 。
的值是 。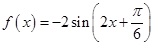 ,下列命题:
,下列命题: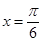 对称;
对称; 个单位,即得到函数
个单位,即得到函数 的图像,
的图像, 中,若
中,若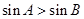 ,则
,则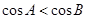 ;
;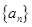 为等差数列,若
为等差数列,若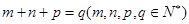 ,则有
,则有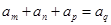 ;
;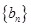 为等比数列,则数列
为等比数列,则数列 、
、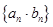 也为等比数列;
也为等比数列;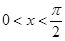 ,则函数
,则函数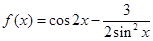 的最大值为
的最大值为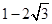 ;
;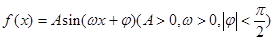 的图象如图所示,则
的图象如图所示,则 ;
;