题目内容
(本小题满分12分)
已知关于 的不等式
的不等式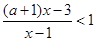 .
.
(Ⅰ)当 时,解该不等式;
时,解该不等式;
(Ⅱ)当 时,解该不等式.
时,解该不等式.
(Ⅰ)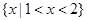 .
.
(Ⅱ)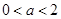 时,解集为
时,解集为 ,
,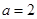 时,解集为
时,解集为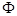 ,
,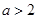 时,解集为
时,解集为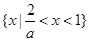
解析试题分析:这是一个含有字母系数的不等式,仔细观察原不等式,通过去分母、移项并合并得到即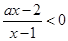 ,等价于
,等价于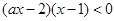 ,然后对于a进行分三类讨论得到。
,然后对于a进行分三类讨论得到。
解:原不等式可化为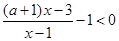 ,即
,即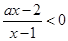 ,等价于
,等价于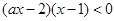
(Ⅰ)当 时,不等式等价于
时,不等式等价于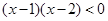 , ∴
, ∴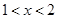
∴原不等式的解集为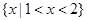 .
.
(Ⅱ)∵原不等式等价于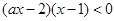 , ∴
, ∴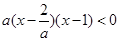
∵ , ∴
, ∴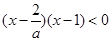
当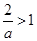 ,即
,即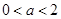 时,解集为
时,解集为
当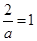 ,即
,即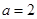 时,解集为
时,解集为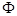
当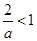 ,即
,即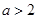 时,解集为
时,解集为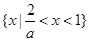
考点:本试题主要考查了不等式性质的灵活运用,以及不等式的等价变形方法一般是移项通分合并,化分式不等式为整式不等式来解得。
点评:该试题主要考查了不等式的性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.注意分三种情况讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在下列函数中,最小值为2的是( )
A. |
B.  |
C. |
D. |
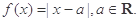
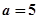 ,解不等式
,解不等式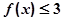 ;
;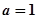 时,若
时,若
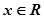 ,使得不等式
,使得不等式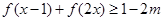 成立,求实数
成立,求实数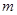 的取值范围.
的取值范围.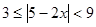
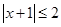 ,
,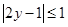 ,求证:
,求证: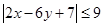 ;
; 满足关系
满足关系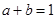 ,求证:
,求证: .
.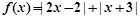 .
.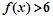 ;
;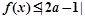 的解集不是空集,试求
的解集不是空集,试求 的取值范围.
的取值范围.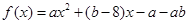 ,当
,当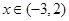 时,
时,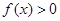 ;
;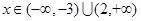 时,
时,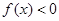 .
.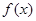 在
在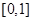 内的值域;
内的值域;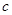 为何值时,
为何值时,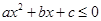 的解集为
的解集为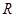 .
. 的不等式:
的不等式: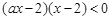
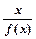 ≤1的解集
≤1的解集 。
。