题目内容
已知函数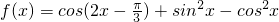 .
.
(I)求出f(x)的最小正周期及函数f(x)图象的对称中心;
(II)设g(x)=f(x+φ),若函数g(x)为偶函数,求满足条件的最小正数φ的值.
解:(I)由题意可得:
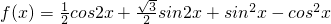
=
=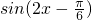 .
.
所以函数的最小正周期 .
.
令 =kπ,
=kπ,
即 (k∈Z).
(k∈Z).
所以函数f(x)图象的对称中心是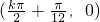 (k∈Z).
(k∈Z).
(II)f(x+φ)=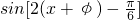 =
= ,
,
因为函数g(x)为偶函数,
所以 (k∈Z).
(k∈Z).
所以 (k∈Z).
(k∈Z).
则满足条件的最小整数φ的值为 .
.
分析:(I)由题意可得:f(x)=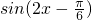 ,根据正弦函数的有关性质可得:函数的最小正周期与函数图象的对称中心.
,根据正弦函数的有关性质可得:函数的最小正周期与函数图象的对称中心.
(II)由题意可得:f(x+φ)=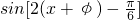 =
= ,根据函数g(x)为偶函数,可得
,根据函数g(x)为偶函数,可得 (k∈Z),进而得到答案.
(k∈Z),进而得到答案.
点评:解决此类问题的关键是熟练掌握正弦函数的有关性质,如单调性,奇偶性,周期性以及对称性等性质.
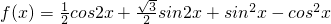
=

=
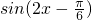 .
.所以函数的最小正周期
 .
.令
 =kπ,
=kπ,即
 (k∈Z).
(k∈Z).所以函数f(x)图象的对称中心是
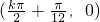 (k∈Z).
(k∈Z).(II)f(x+φ)=
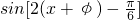 =
= ,
,因为函数g(x)为偶函数,
所以
 (k∈Z).
(k∈Z).所以
 (k∈Z).
(k∈Z).则满足条件的最小整数φ的值为
 .
.分析:(I)由题意可得:f(x)=
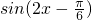 ,根据正弦函数的有关性质可得:函数的最小正周期与函数图象的对称中心.
,根据正弦函数的有关性质可得:函数的最小正周期与函数图象的对称中心.(II)由题意可得:f(x+φ)=
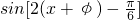 =
= ,根据函数g(x)为偶函数,可得
,根据函数g(x)为偶函数,可得 (k∈Z),进而得到答案.
(k∈Z),进而得到答案.点评:解决此类问题的关键是熟练掌握正弦函数的有关性质,如单调性,奇偶性,周期性以及对称性等性质.

练习册系列答案
相关题目
 .
. .
. .
. .
.