题目内容
在棱长为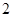 的正方体
的正方体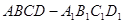 中,
中,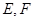 分别为
分别为 的中点.
的中点.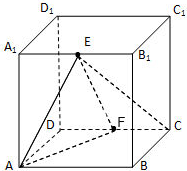
(1)求直线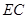 与平面
与平面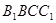 所 成 角的大小;
所 成 角的大小;
(2)求二面角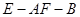 的大小.
的大小.
(1) 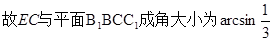 (2)
(2) 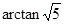
解析试题分析:(1)解法一:建立坐标系
平面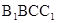 的一个法向量为
的一个法向量为
因为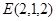
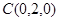 ,
, ,
,
可知直线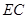 的一个方向向量为
的一个方向向量为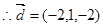 .
.
设直线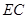 与平面
与平面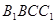 成角为
成角为 ,
, 与
与 所成角为
所成角为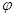 ,则
,则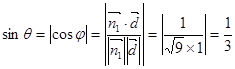
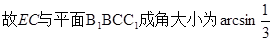
解法二: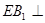 平面
平面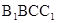 ,即
,即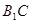 为
为 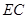 在平面
在平面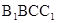 内的射影,
内的射影,
故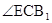 为直线
为直线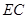 与平面
与平面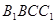 所成角,
所成角,
在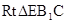 中,
中,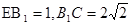 ,
,

(2)解法一:建立坐标系如图.平面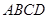 的一个法向量为
的一个法向量为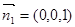
设平面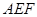 的一个法向量为
的一个法向量为 ,因为
,因为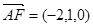 ,
,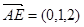
所以 ,令
,令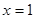 ,则
,则
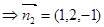
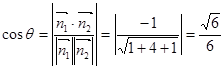
由图知二面角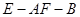 为锐二面角,故其大小为
为锐二面角,故其大小为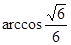 .
.
解法二:过 作平面
作平面 的垂线,垂足为
的垂线,垂足为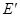 ,
,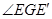 即为所求
即为所求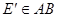 ,过
,过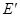 作
作 的垂线设垂足为
的垂线设垂足为 ,
,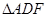 ∽
∽
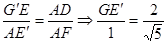 即
即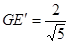 在
在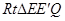 中
中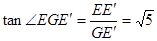
所以 二面角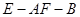 的大小为
的大小为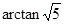 .
.
考点:空间中角的求解
点评:解决的关键是利用角的定义作图来结合几何中的性质定理和判定定理来得到,解三角形得到,或者建立空间直角坐标系,运用向量法来求解。属于中档题。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 是正方形,
是正方形,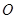 为对角线
为对角线 和
和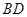 的交点,
的交点, ,
,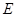 为
为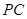 的中点;
的中点;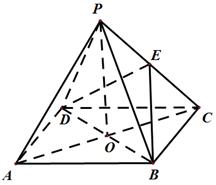
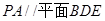 ;
;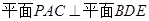 .
.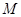 ,
, 分别是
分别是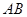 ,
, 的中点.
的中点.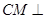 平面
平面 ;
;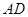 上(含
上(含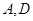 端点)确定一点
端点)确定一点 ,使得
,使得 ∥平面
∥平面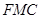 ,并给出证明.
,并给出证明.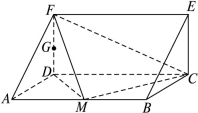
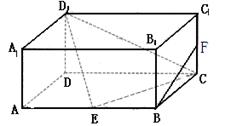
 中,
中,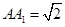 ,
, ,
, 是底面对角线的交点.
是底面对角线的交点.
 平面
平面 ;
; 平面
平面 的体积。
的体积。 AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.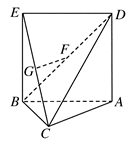


 中,
中, 点
点 在棱
在棱 上.
上.
 与
与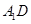 所成的角;
所成的角; 的大小为
的大小为 ,求点
,求点 到面
到面 的距离.
的距离.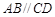 ,
,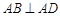 ,且
,且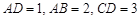 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且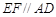 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为 .
.
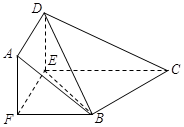
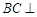 平面BDE;
平面BDE;