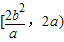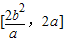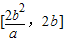题目内容
如图，已知椭圆方程为| x2 |
| a2 |
| y2 |
| b2 |
分析：确定以OM为直径的圆与以椭圆长轴为直径的圆的方程，利用图形的对称性，即可求得结论．
解答：解：设M（
，m），则以OM为直径的圆的方程为(x-
)2+(y-
)2=
+
①
以椭圆长轴为直径的圆的方程为x2+y2=a2②
根据图形可知，当M在x轴上时，|AB|最小，此时方程①为(x-
)2+y2=
③
②-③可得：x=c，代入椭圆方程，可得
+
=1，∴y=±
，∴|AB|=
当M在无穷远时，|AB|最大，以OM为直径的圆与以椭圆长轴为直径的圆交于长轴的端点，∴|AB|→2a
∴|AB|的取值范围是[
，2a)
故选A．
| a2 |
| c |
| a2 |
| 2c |
| m |
| 2 |
| a4 |
| 4c2 |
| m2 |
| 4 |
以椭圆长轴为直径的圆的方程为x2+y2=a2②
根据图形可知，当M在x轴上时，|AB|最小，此时方程①为(x-
| a2 |
| 2c |
| a4 |
| 4c2 |
②-③可得：x=c，代入椭圆方程，可得
| c2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| 2b2 |
| a |
当M在无穷远时，|AB|最大，以OM为直径的圆与以椭圆长轴为直径的圆交于长轴的端点，∴|AB|→2a
∴|AB|的取值范围是[
| 2b2 |
| a |
故选A．
点评：本题考查圆的方程，考查圆与椭圆的综合，解题的关键是确定圆的方程，属于中档题．
练习册系列答案
相关题目
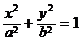（a>b>0），焦点为F1，F2，P是椭圆上一点，∠F1PF2=α,求△F1PF2的面积（用a、b、α表示）．
分别为其左右焦点，A为左顶点，直线l的方程为x=4，过F2的直线l′与椭圆交于异于A的P、Q两点．
的取值范围；
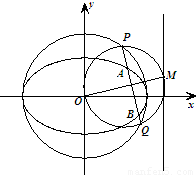
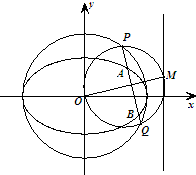
求证：M、N两点的纵坐标之积为定值；并求出该定值．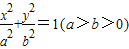
，O为原点，点M是椭圆右准线上的动点，以OM为直径的圆与以椭圆长轴为直径的圆交于P、Q两点，直线PQ与椭圆相交于A、B两点，则|AB|的取值范围是（ ）
，F1、F2分别为椭圆的左、右焦点，A为椭圆的一顶点，直线AF2交椭圆于点B．
90°，求椭圆的离心率；
，求椭圆的方程． 