题目内容
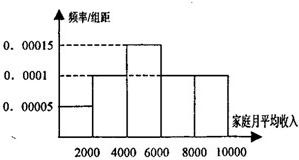
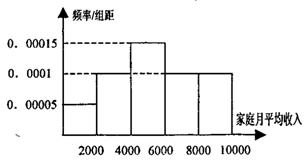
某校调查了高三年级1000位同学的家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图.(1)某企业准备给该校高三同学发放助学金,发放规定如下:家庭收入在4000元以下的每位同学得助学金2000元,家庭收入在(4000,6000](元)间的每位同学得助学金1500元,家庭收入在(6000,8000](元)间的每位同学得助学金1000元,家庭收入在(8000,10000](元),间的同学不发助学金,记该年级某位同学所得助学金为ξ元,写出ξ的分布列,并计算该企业发放这个年级的助学金约需要的资金;
(2)记该年级某班同桌两位同学所得助学金之差的绝对值为η元,求P(η>500).

【答案】分析:(1)欲求:“计算该企业发放这个年级的助学金约需要的资金”,先列出ξ的分布列后求每一位同学所须资金的数学期望值,最后乘以1000即可;
(2)事件:“η>500”可分解成三类讨论,即:η=1000,或η=1500或η=2000,分别求出它们的概率,最后求和即可.
解答:解:(1)ξ的分布列是

Eξ=2000×0.3+1500×0.3+1000×0.2+0×0.2=1250(元)
所以需要资金约为:1250×1000=1250000(元);(6分)
(2)P(η=1000)=2×0.2×0.2+2×0.3×0.2=0.2,(8分)
P(η=1500)=2×0.3×0.2=0.12,(9分)
P(η=2000)=2×0.3×0.2=0.12,(10分)
所以P(η>500)=0.2+0.12+0.12=0.44.(12分)
点评:本题主要考查频率分布直方图和离散型随机变量及其分布列,是一道离散型随机变量及其分布列与频率分布直方图交汇的题目.
(2)事件:“η>500”可分解成三类讨论,即:η=1000,或η=1500或η=2000,分别求出它们的概率,最后求和即可.
解答:解:(1)ξ的分布列是

Eξ=2000×0.3+1500×0.3+1000×0.2+0×0.2=1250(元)
所以需要资金约为:1250×1000=1250000(元);(6分)
(2)P(η=1000)=2×0.2×0.2+2×0.3×0.2=0.2,(8分)
P(η=1500)=2×0.3×0.2=0.12,(9分)
P(η=2000)=2×0.3×0.2=0.12,(10分)
所以P(η>500)=0.2+0.12+0.12=0.44.(12分)
点评:本题主要考查频率分布直方图和离散型随机变量及其分布列,是一道离散型随机变量及其分布列与频率分布直方图交汇的题目.

练习册系列答案
相关题目