题目内容
已知f(θ)=1-2sinθ,g(θ)=3-4cos2θ.记F(θ)=a•f(θ)+b•g(θ)(其中a,b都为常数,且b>0).(Ⅰ)若a=4,b=1,求F(θ)的最大值及此时的θ值;
(Ⅱ)若
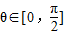 ,①证明:F(θ)的最大值是|2b-a|+b;②证明:F(θ)+|2b-a|+b≥0.
,①证明:F(θ)的最大值是|2b-a|+b;②证明:F(θ)+|2b-a|+b≥0.
【答案】分析:(Ⅰ)将a与b的值代入利用同角三角函数间的基本关系化简,整理后利用二次函数的性质即可求出F(θ)的最大值及此时的θ值;
(Ⅱ)F(θ)解析式利用同角三角函数间的基本关系整理后,设sinθ=x,得到G(x)关于x的二次函数关系式,利用二次函数的性质求出抛物线的对称轴,
①当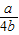 ≤
≤ ,即2b≥a时,求出G(x)的最大值为G(1),当
,即2b≥a时,求出G(x)的最大值为G(1),当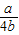 >
> ,即2b<a时,G(x)的最大值G(0),即可得证;
,即2b<a时,G(x)的最大值G(0),即可得证;
②要证F(θ)+|2b-a|+b≥0,即求证G(x)min+|2b-a|+b≥0,其中G(x)=4b(x-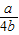 )2+a-b-
)2+a-b-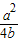 (0≤x≤1),
(0≤x≤1),
当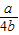 <0,即a<0时,G(x)min+|2b-a|+b大于0,当0≤
<0,即a<0时,G(x)min+|2b-a|+b大于0,当0≤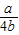 ≤1,0≤a≤4b时,G(x)min+|2b-a|+b也大于0,得证.
≤1,0≤a≤4b时,G(x)min+|2b-a|+b也大于0,得证.
解答:解:(Ⅰ)若a=4,b=1时,F(θ)=4(1-2sinθ)+3-4cos2θ=4(sinθ-1)2-1,
则F(θ)max=15,此时的θ=2kπ-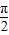 (k∈Z);
(k∈Z);
(Ⅱ)证明:F(θ)=a(1-2sinθ)+b(3-4cos2θ)=4b(sinθ-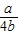 )2+a-b-
)2+a-b-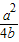 ,
,
令sinθ=x∈[0,1],记G(x)=4b(x-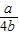 )2+a-b-
)2+a-b-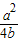 (0≤x≤1),
(0≤x≤1),
则其对称轴x=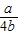 ;
;
①当 ≤
≤ ,即2b≥a时,G(x)max=G(1)=3b-a;
,即2b≥a时,G(x)max=G(1)=3b-a;
当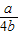 >
> ,即2b<a时,G(x)max=G(0)=a-b,
,即2b<a时,G(x)max=G(0)=a-b,
则G(x)max=F(θ)max=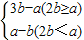 =|2b-a|+b;
=|2b-a|+b;
②F(θ)+|2b-a|+b≥0,即求证G(x)min+|2b-a|+b≥0,
其中G(x)=4b(x-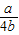 )2+a-b-
)2+a-b-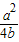 (0≤x≤1),
(0≤x≤1),
当 <0,即a<0时,G(x)min+|2b-a|+b=G(0)+2b-a+b=2b>0,
<0,即a<0时,G(x)min+|2b-a|+b=G(0)+2b-a+b=2b>0,
当0≤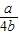 ≤1,即0≤a≤4b时,G(x)min+|2b-a|+b=G(
≤1,即0≤a≤4b时,G(x)min+|2b-a|+b=G(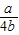 )+|2b-a|+b=a-b-
)+|2b-a|+b=a-b-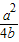 +|2b-a|+b
+|2b-a|+b
=a-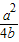 +|2b-a|=
+|2b-a|=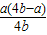 +|2b-a|≥0,
+|2b-a|≥0,
当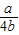 >1,即a>4b时,G(x)min+|2b-a|+b=G(1)+a-2b+b=2b>0,
>1,即a>4b时,G(x)min+|2b-a|+b=G(1)+a-2b+b=2b>0,
综上:F(θ)+|2b-a|+b≥0.
点评:此题考查了两角和与差的正弦函数公式,函数最值的应用,以及正弦函数的定义域与值域,熟练掌握公式是解本题的关键.
(Ⅱ)F(θ)解析式利用同角三角函数间的基本关系整理后,设sinθ=x,得到G(x)关于x的二次函数关系式,利用二次函数的性质求出抛物线的对称轴,
①当
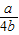 ≤
≤ ,即2b≥a时,求出G(x)的最大值为G(1),当
,即2b≥a时,求出G(x)的最大值为G(1),当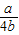 >
> ,即2b<a时,G(x)的最大值G(0),即可得证;
,即2b<a时,G(x)的最大值G(0),即可得证;②要证F(θ)+|2b-a|+b≥0,即求证G(x)min+|2b-a|+b≥0,其中G(x)=4b(x-
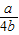 )2+a-b-
)2+a-b-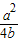 (0≤x≤1),
(0≤x≤1),当
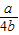 <0,即a<0时,G(x)min+|2b-a|+b大于0,当0≤
<0,即a<0时,G(x)min+|2b-a|+b大于0,当0≤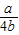 ≤1,0≤a≤4b时,G(x)min+|2b-a|+b也大于0,得证.
≤1,0≤a≤4b时,G(x)min+|2b-a|+b也大于0,得证.解答:解:(Ⅰ)若a=4,b=1时,F(θ)=4(1-2sinθ)+3-4cos2θ=4(sinθ-1)2-1,
则F(θ)max=15,此时的θ=2kπ-
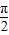 (k∈Z);
(k∈Z);(Ⅱ)证明:F(θ)=a(1-2sinθ)+b(3-4cos2θ)=4b(sinθ-
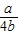 )2+a-b-
)2+a-b-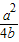 ,
,令sinθ=x∈[0,1],记G(x)=4b(x-
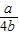 )2+a-b-
)2+a-b-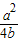 (0≤x≤1),
(0≤x≤1),则其对称轴x=
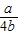 ;
;①当
 ≤
≤ ,即2b≥a时,G(x)max=G(1)=3b-a;
,即2b≥a时,G(x)max=G(1)=3b-a;当
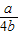 >
> ,即2b<a时,G(x)max=G(0)=a-b,
,即2b<a时,G(x)max=G(0)=a-b,则G(x)max=F(θ)max=
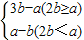 =|2b-a|+b;
=|2b-a|+b;②F(θ)+|2b-a|+b≥0,即求证G(x)min+|2b-a|+b≥0,
其中G(x)=4b(x-
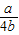 )2+a-b-
)2+a-b-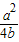 (0≤x≤1),
(0≤x≤1),当
 <0,即a<0时,G(x)min+|2b-a|+b=G(0)+2b-a+b=2b>0,
<0,即a<0时,G(x)min+|2b-a|+b=G(0)+2b-a+b=2b>0,当0≤
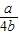 ≤1,即0≤a≤4b时,G(x)min+|2b-a|+b=G(
≤1,即0≤a≤4b时,G(x)min+|2b-a|+b=G(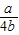 )+|2b-a|+b=a-b-
)+|2b-a|+b=a-b-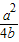 +|2b-a|+b
+|2b-a|+b=a-
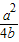 +|2b-a|=
+|2b-a|=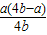 +|2b-a|≥0,
+|2b-a|≥0,当
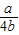 >1,即a>4b时,G(x)min+|2b-a|+b=G(1)+a-2b+b=2b>0,
>1,即a>4b时,G(x)min+|2b-a|+b=G(1)+a-2b+b=2b>0,综上:F(θ)+|2b-a|+b≥0.
点评:此题考查了两角和与差的正弦函数公式,函数最值的应用,以及正弦函数的定义域与值域,熟练掌握公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目