题目内容
求五次多项式f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0,当x=x0(x0为任意实数)时的值.
f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0=((((a5x+a4)x+a3)x+a2)x+a1)x+a0.
算法步骤如下:
第一步 计算最内层a5x+a4的值,把a5x+a4的值赋给一个变量v1;
第二步 计算(a5x+a4)x+a3的值,可以改写为v1x+a3,把v1x+a3的值赋给一个变量v2;
第三步 计算((a5x+a4)x+a3)x+a2的值,则该式子可改写为v2x+a2,把v2x+a2的值赋给一个变量v3;
第四步 计算(((a5x+a4)x+a3)x+a2)x+a1,则该式子可改写为v3x+a1,把v3x+a1的值赋给一个变量v4;
第五步 计算((((a5x+a4)x+a3)x+a2)x+a1)x+a0,则该式子可改写为v4x+a0.
以上过程可简写为
v0=a5,
v1=v0x+a4,
v2=v1x+a3,
v3=v2x+a2,
v4=v3x+a1,
v5=v4x+a0.
算法步骤如下:
第一步 计算最内层a5x+a4的值,把a5x+a4的值赋给一个变量v1;
第二步 计算(a5x+a4)x+a3的值,可以改写为v1x+a3,把v1x+a3的值赋给一个变量v2;
第三步 计算((a5x+a4)x+a3)x+a2的值,则该式子可改写为v2x+a2,把v2x+a2的值赋给一个变量v3;
第四步 计算(((a5x+a4)x+a3)x+a2)x+a1,则该式子可改写为v3x+a1,把v3x+a1的值赋给一个变量v4;
第五步 计算((((a5x+a4)x+a3)x+a2)x+a1)x+a0,则该式子可改写为v4x+a0.
以上过程可简写为
v0=a5,
v1=v0x+a4,
v2=v1x+a3,
v3=v2x+a2,
v4=v3x+a1,
v5=v4x+a0.
同答案

练习册系列答案
相关题目

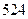 转化为八进制数为_______。
转化为八进制数为_______。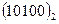 转化为十进制数得________
转化为十进制数得________