Question

一次高中数学期末考试，选择题共有个，每个选择题给出了四个选项，在给出的四个选项中，只有一项是符合题目要求的. 评分标准规定：对于每个选择题，不选或多选或错选得分，选对得分．在这次考试的选择题部分，某考生比较熟悉其中的个题，该考生做对了这个题．其余个题，有一个题，因全然不理解题意，该考生在给出的四个选项中，随机选了一个；有一个题给出的四个选项，可判断有一个选项不符合题目要求，该考生在剩下的三个选项中，随机选了一个；还有两个题，每个题给出的四个选项，可判断有两个选项不符合题目要求，对于这两个题，该考生都是在剩下的两个选项中，随机选了一个选项．请你根据上述信息，解决下列问题：

（Ⅰ）在这次考试中，求该考生选择题部分得分的概率；

（Ⅱ）在这次考试中，设该考生选择题部分的得分为，求的数学期望．

 

Answer 1

【答案】

（Ⅰ）;（Ⅱ）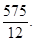

【解析】

试题分析：1.本题以学生熟悉的背景设题，将得分与选择对、选错联系起来，感受随机事件与概率．因此，解题首先是要读懂题意.善于在熟悉的情境中理解题意，这是解概率题的关键．2.概率问题往往涉及到分类计算，这是由于分布列的特点需要分类进行计算．另由于选择各题时相对独立，独立事件也需要分类计算．3．概率题要求计算要准确，全功尽弃.

试题解析：设选对“全然不理解题意”的试题的选项为事件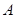，选对“可判断有一个选项不符合题目要求”

试题的选项为事件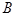，选对“可判断有两个选项不符合题目要求”试题的选项为事件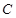，根据题意

，，.

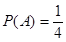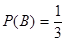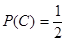（Ⅰ）在这次考试中，该考生选择题得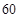分的概率；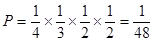

（Ⅱ）随机变量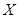可能的取值为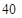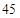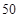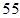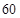，，，，，根据题意得

，

，

              ，

，

.

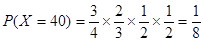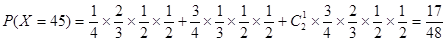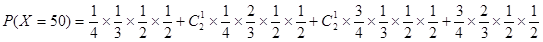
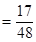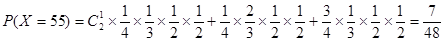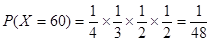∴的数学期望.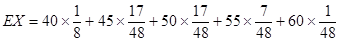

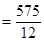考点：概率,随机变量分布列、数学期望的计算.