题目内容
(本大题共15分)已知![]() 在
在![]() 上是增函数,
上是增函数,![]() 在
在![]() 上是减函数.(1)求
上是减函数.(1)求![]() 的值;(2)设函数
的值;(2)设函数![]() 在
在![]() 上是增函数,且对于
上是增函数,且对于![]() 内的任意两个变量
内的任意两个变量![]() ,恒有
,恒有![]() 成立,求实数
成立,求实数![]() 的取值范围;(3)设
的取值范围;(3)设![]() ,求证:
,求证:![]() .
.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() . (Ⅲ)
. (Ⅲ)![]()
解析:
:(1)![]() ,依题意,当
,依题意,当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() .
.
![]() ,当
,当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() ,所以
,所以![]() .…………5分
.…………5分
(2)![]() ,所以
,所以![]() 在
在![]() 上是减函数,最小值是
上是减函数,最小值是![]() .
.
![]() 在
在![]() 上是增函数,即
上是增函数,即![]() 恒成立,得
恒成立,得![]() ,且
,且![]() 的最大值是
的最大值是![]() ,由已知得
,由已知得![]()
![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .…………5分
.…………5分
(3) ![]() ,
,
方法一:
![]() 时不等式左右相等,得证;
时不等式左右相等,得证;
![]() 时,
时,![]()
![]() ,
,
所以![]() 成立. ……5分
成立. ……5分
方法二:
用数学归纳法很快可证,方法很好.证明略.

练习册系列答案
相关题目
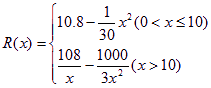 .
.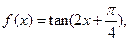 ,
,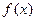 的定义域与最小正周期;
的定义域与最小正周期; ,若
,若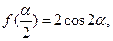 求
求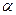 的大小.
的大小.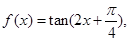 ,
,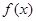 的定义域与最小正周期;
的定义域与最小正周期;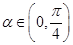 ,若
,若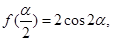 求
求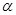 的大小.
的大小. .
.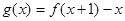 的最大值;
的最大值;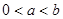 时,求证
时,求证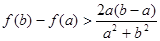 .
.