题目内容
已知数列{an}是公比q≠1的等比数列,则在“(1){anan+1},(2){an+1-an},(3){an3},(4){nan}”这四个数列中,成等比数列的个数是
- A.1
- B.2
- C.3
- D.4
C
分析:利用等比数列的定义,逐个数列进行判断,得出正确结果个数即可.
解答:{an}是公比q≠1的等比数列,则有 =q (q≠1)
=q (q≠1)
对于数列{anan+1},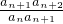 =
=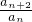 =q2,是定值,成等比数列.
=q2,是定值,成等比数列.
对于数列 {an+1-an},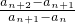 =
=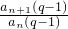 =
= =q,是定值,成等比数列.
=q,是定值,成等比数列.
对于数列{an3}, =
=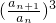 =q3,是定值,成等比数列.
=q3,是定值,成等比数列.
对于数列{nan}, =
= •
• =
= q,是与n有关的变量,不成等比数列.
q,是与n有关的变量,不成等比数列.
成等比数列的个数是3个.
故选C.
点评:本题考查等比数列的判断方法,利用了定义进行判定.是基础题.
分析:利用等比数列的定义,逐个数列进行判断,得出正确结果个数即可.
解答:{an}是公比q≠1的等比数列,则有
 =q (q≠1)
=q (q≠1)对于数列{anan+1},
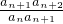 =
=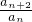 =q2,是定值,成等比数列.
=q2,是定值,成等比数列.对于数列 {an+1-an},
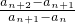 =
=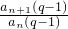 =
= =q,是定值,成等比数列.
=q,是定值,成等比数列.对于数列{an3},
 =
=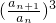 =q3,是定值,成等比数列.
=q3,是定值,成等比数列.对于数列{nan},
 =
= •
• =
= q,是与n有关的变量,不成等比数列.
q,是与n有关的变量,不成等比数列.成等比数列的个数是3个.
故选C.
点评:本题考查等比数列的判断方法,利用了定义进行判定.是基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目