题目内容
在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() . 以
. 以![]() 的中点
的中点![]() 为球心、
为球心、![]() 为直径的球面交
为直径的球面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;![]()
![]()
(2)求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
20.解:
方法一:(1)依题设知,AC是所作球面的直径,则AM⊥MC。
又因为P A⊥平面ABCD,则PA⊥CD,又CD⊥AD,
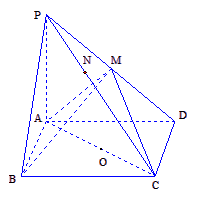 http://www.ks5u.com/所以CD⊥平面PAD,则CD⊥AM,所以A M⊥平面PCD,
http://www.ks5u.com/所以CD⊥平面PAD,则CD⊥AM,所以A M⊥平面PCD,
所以平面ABM⊥平面PCD。
(2)由(1)知,![]() ,又
,又![]() ,则
,则![]() 是
是![]() 的中点可得
的中点可得
![]() ,
,![]()
则![]()
设D到平面ACM的距离为![]() ,由
,由![]() 即
即![]() ,
,
可求得![]() ,
,
设所求角为![]() ,则
,则![]() ,
,![]() 。
。
(1) 可求得PC=6。因为AN⊥NC,由![]() ,得PN
,得PN![]() 。所以
。所以![]() 。
。
故N点到平面ACM的距离等于P点到平面ACM距离的![]() 。
。
又因为M是PD的中点,则P、D到平面ACM的距离相等,由(2)可知所求距离为![]() 。
。
方法二:
 (1)同方法一;
(1)同方法一;
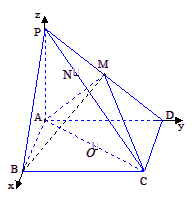
(2)如图所示,建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ;设平面
;设平面![]() 的一个法向量
的一个法向量![]() ,由
,由![]() 可得:
可得:![]() ,令
,令![]() ,则
,则
![]() 。设所求角为
。设所求角为![]() ,则
,则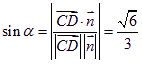 ,
,
所以所求角的大小为![]() 。
。
(2) 由条件可得,![]() .在
.在![]() 中,
中,![]() ,所以
,所以![]() ,则
,则![]() ,
, ![]() ,所以所求距离等于点
,所以所求距离等于点![]() 到平面
到平面![]() 距离的
距离的![]() ,设点
,设点![]() 到平面
到平面![]() 距离为
距离为![]() 则
则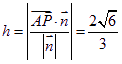 ,所以所求距离为
,所以所求距离为![]() 。
。
解析:
⑴略,⑵![]() ,⑶
,⑶![]()

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目


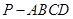 中,底面
中,底面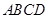 是矩形,
是矩形,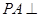 平面
平面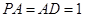 ,
,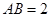 ,
,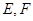 分别是
分别是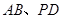 的中点.
的中点.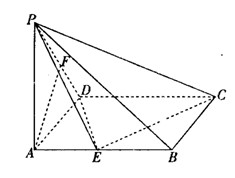
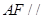 平面
平面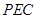 ;
;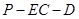 的余弦值.
的余弦值.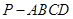 中,底面
中,底面 是矩形,四条侧棱长均相等.
是矩形,四条侧棱长均相等.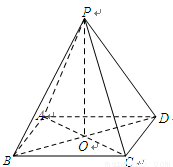
 平面
平面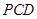 ;
;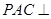 平面
平面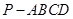 中,底面
中,底面 是矩形,
是矩形,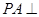 平面
平面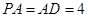 ,
,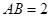 .以
.以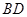 的中点
的中点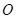 为球心、
为球心、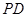 于点
于点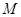 .
.
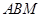 ;
;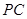 与平面
与平面