题目内容
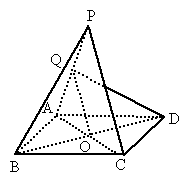
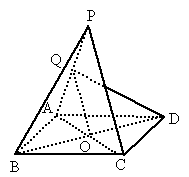
如图,P是平行四边形ABCD所在平面外一点;Q是PA的中点,求证:PC∥平面BQD.
答案:略
解析:
提示:
解析:
|
连接 AC、BD交于O,连QO,∵ ABCD为平行四边形∴ O为AC的中点,∴ QO∥PC又 PC 平面BQD,QO 平面BQD,QO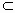 平面BQD. 平面BQD.
∴ PC∥平面BQD. |
提示:
|
证明“线∥面”一般通过“线∥线”来实现. 证明“线∥面”关键是在平面 BQD内找到一条直线与已知直线平行,怎么找呢?一般按两步法即“先找线后连线”,找线即在平面内现有的直线中发现,若找线不成再在平面内添加辅助线,辅助线一般连接特殊点(中点、三等分点等)添加,多为中线、高线、中位线等.此题中的QO既是△BQD的中线,又是△PAC的中位线. |

练习册系列答案
相关题目