题目内容
若任意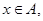 则
则 就称
就称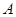 是“和谐”集合.则在集合
是“和谐”集合.则在集合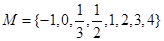 的所有非空子集中,“和谐”集合的个数有 个.
的所有非空子集中,“和谐”集合的个数有 个.
15
解析试题分析:由定义,任意x∈A,则 ,就称A是“和谐”集合,知此类集合中的元素互为倒数成对出现,观察集合M,互为倒数的数有4对, 1与1,-1与-1,2与
,就称A是“和谐”集合,知此类集合中的元素互为倒数成对出现,观察集合M,互为倒数的数有4对, 1与1,-1与-1,2与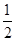 ,3与
,3与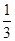 ,
,
可将这些数看作是四个元素,由于包括四个元素的集合的非空子集是24-1=15。
考点:本题主要考查集合的真子集数计算方法,学习能力。
点评:简单题,解题的关键是理解所给的定义及集合的真子集的个数计算方法,求出集合的真子集个数即和谐集合的个数。

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
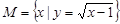 ,则
,则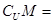 .
.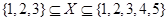 的集合
的集合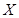 的个数为:
的个数为:  的定义域为集合
的定义域为集合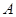 ,
,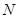 为自然数集,则
为自然数集,则 = .
= . ,则
,则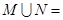
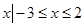 },B={x
},B={x },且A
},且A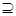 B,实数k的取值范围是 。
B,实数k的取值范围是 。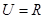 ,集合
,集合 ,则
,则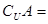
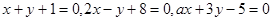 不能围成三角形,则
不能围成三角形,则 的取值集合是 _
的取值集合是 _ 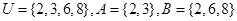 ,则
,则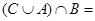 ________
________