题目内容
已知P是椭圆
＝1(a＞b＞0)上的点，P与两焦点F1、F2的连线互相垂直，且点P到两准线的距离分别为d1＝6和d2＝12，求椭圆方程．
答案：
解析：
解析：
|
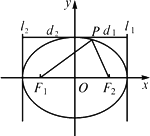
解析：如图所示：P到l1的距离为d1，P到l2的距离为d2，
由圆锥曲线的统一定义知：|PF1|＝ed1，|PF2|＝ed2 又∵|PF1|2＋|PF2|2＝|FF2|2， ∴ ∴ a2＝ 又∵|PF1|＋|PF2|＝2a ∴|PF1|2＋2|PF1||PF2|＋|PF2|2＝4a2， ∴4c2＋2e2d1d2＝4a2， ∴4c2＋ ∴4c2＋ ∴ ∴c＝ ∴椭圆方程为： |
＝(2c)2，
(62＋122)＝4c2
＝45．
＝4a2．
＝45×4
＝45，∴c2＝
＝5 ∴c2＝25 ∴b2＝a2－c2＝20．
＝1．
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
＝1(a＞b＞0)上一点，
是椭圆的焦点，
，且点P到两准线的距离分别为
)、C(
)，Q(
)是椭圆上一动点(
＞0)，QH⊥x轴，垂足为H，∠BQH＝α，∠HQC＝β．
+
＝1上的一点, P到一条准线的距离与P到相应焦点的距离之比为
B.
C.
D.
＝1上的点，Q、R分别是圆(x＋4)2＋y2＝
和圆(x－4)2＋y2＝
上的点，则|PQ|＋|PR|的最小值是
＝1上的一点，F1、F2是该椭圆的两个焦点，若△PF1F2的内切圆半径为
，则
的值为
