题目内容
已知.f(x)=loga(1-x)(a>0,a≠1),g(x)=loga(1+x)(a>0,且a≠1)
(1)求函数f(x)+g(x)的定义域;
(2)求使f(x)>0成立的x的取值范围.
(1)求函数f(x)+g(x)的定义域;
(2)求使f(x)>0成立的x的取值范围.
分析:(1)求出函数f(x)与函数g(x)的定义域,然后求出交集即可;
(2)利用对数的运算法则化简f(x)>0通过a的范围求解不等式成立的x的取值范围.
(2)利用对数的运算法则化简f(x)>0通过a的范围求解不等式成立的x的取值范围.
解答:解:(1)依题意得1-x>0且1+x>0 (1分)
解得x<1且x>-1 (2分)
故所求定义域为{x|-1<x<1}…(4分)
(2)由f(x)>0
得loga(1-x)>loga1(6分)
当a>1时,1-x>1即x<0(8分)
当0<a<1时,0<1-x<1即0<x<1(10分)
综上,当a>1时,x的取值范围是{x|x<0},当0<a<1时,x的取值范围是{x|0<x<1}…(12分)
解得x<1且x>-1 (2分)
故所求定义域为{x|-1<x<1}…(4分)
(2)由f(x)>0
得loga(1-x)>loga1(6分)
当a>1时,1-x>1即x<0(8分)
当0<a<1时,0<1-x<1即0<x<1(10分)
综上,当a>1时,x的取值范围是{x|x<0},当0<a<1时,x的取值范围是{x|0<x<1}…(12分)
点评:本题考查分类讨论思想的应用,函数的定义域,不等式的解法,考查计算能力.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 )2+7lo
)2+7lo +3≤0的解集为M,求当x∈M时,函数f(x)=(lo
+3≤0的解集为M,求当x∈M时,函数f(x)=(lo )(lo
)(lo )的最大值和最小值.
)的最大值和最小值.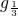 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.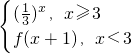 ,则f(2+lo
,则f(2+lo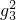 )的值为________.
)的值为________. [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.