题目内容
分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0”,求证
<
a”索的因应是( )
| b2-ac |
| 3 |
分析:由题意可得,要证
<
a,经过分析,只要证(a-c)(a-b)>0,从而得出结论.
| b2-ac |
| 3 |
解答:解:由a>b>c,且a+b+c=0可得 b=-a-c,a>0,c<0.
要证
<
a,只要证 (-a-c)2-ac<3a2,
即证 a2-ac+a2-c2>0,即证a(a-c)+(a+c)(a-c)>0,
即证 a(a-c)-b(a-c)>0,即证(a-c)(a-b)>0.
故求证“
<
a”索的因应是 (a-c)(a-b)>0,
故选C.
要证
| b2-ac |
| 3 |
即证 a2-ac+a2-c2>0,即证a(a-c)+(a+c)(a-c)>0,
即证 a(a-c)-b(a-c)>0,即证(a-c)(a-b)>0.
故求证“
| b2-ac |
| 3 |
故选C.
点评:本题主要考查用分析法证明不等式,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
 ”索的因应是( )
”索的因应是( )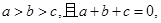 求证
求证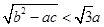 ”索的因应是( )
”索的因应是( )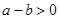 B
B
 C
C
 D
D
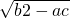 <
< a”索的因应是
a”索的因应是