题目内容
点P(-3,1)在椭圆 的左准线上,过点P斜率为
的左准线上,过点P斜率为 的光线,
的光线,
经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为
A. | B. | C. | D. |
A
解析

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
.如图所示,从双曲线-=1(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切
点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|-
|MT|与b-a的大小关系为 ( )
| A.|MO|-|MT|>b-a | B.|MO|-|MT|=b-a |
| C.|MO|-|MT|<b-a | D.不确定 |
如图,圆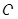 的半径为定长
的半径为定长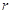 ,
,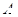 是圆
是圆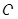 外一个定点,
外一个定点,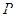 是圆上任意一点,线段
是圆上任意一点,线段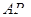 的垂直平分线
的垂直平分线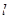 和直线
和直线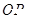 相交于点
相交于点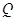 ,当点
,当点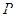 在圆上运动时,点
在圆上运动时,点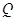 的轨迹是( )
的轨迹是( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且和y轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线的方程为( )
| A.y2=±4x | B.y2=±8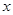 | C.y2=4x | D.y2=8x |
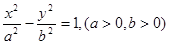 右支上一点,
右支上一点,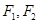 ,分别是双曲线的左、右焦点,I为
,分别是双曲线的左、右焦点,I为 的内心,若
的内心,若 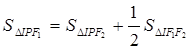 成立,则双曲线的离心率为( )
成立,则双曲线的离心率为( )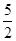
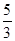
 B
B  C
C  D
D 
 的左右焦点分别为
的左右焦点分别为 ,过焦点
,过焦点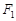 的倾斜角为
的倾斜角为 直线交椭圆于A,B两点,弦长
直线交椭圆于A,B两点,弦长 ,若三角形ABF2的内切圆的面积为
,若三角形ABF2的内切圆的面积为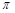 ,则椭圆的离心率为 ( )
,则椭圆的离心率为 ( )
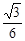

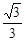
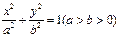 中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2
中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2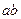 B.
B.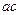 C.
C.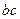 D.
D.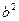
 ,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于
,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于 点Q,则点Q(x,y)所满足的轨迹方程为 ( ▲ )
点Q,则点Q(x,y)所满足的轨迹方程为 ( ▲ )


