题目内容
20.设m,n,l为空间不重合的直线,α,β,γ是空间不重合的平面,则下列说法准确的个数是( )①m∥l,n∥l,则m∥n;②m⊥l,n⊥l,则m∥n;③若m∥l,m∥α,则l∥α; ④若l∥m,l?α,m?β,则α∥β;⑤若m?α,m∥β,l?β,l∥α,则α∥β⑥α∥γ,β∥γ,则α∥β.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 要判断线线、线面、面面的位置关系,要根据线面平行(垂直)、面面平行(垂直)的判定和性质,八个定理来判断.
解答 解:①若m∥l,n∥l,则m∥n,根据公理4:平行于同一直线的两只线平行,所以①正确;
②由m⊥l,n⊥l,在同一个平面可得m∥n,在空间不成立,故错误;
③若m∥l,m∥α则l∥α或l?α,故错误;
④若α∩β=a且m∥a∥l,此时α∥β不成立.故错误;
⑤若α∩β=a且m∥a∥l,此时α∥β不成立.故错误;
⑥α∥γ,β∥γ,利用平面与平面平行的性质与判定,可得α∥β,正确.
故选:C.
点评 此题考查学生对空间中点、线、面的位置关系的理解与掌握.重点考查学生的空间想象能力.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
11.在棱长为1的正方体ABCD-A1B1C1D1中,B1点到平面ACD1的距离为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
5.如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ:BC等于( )
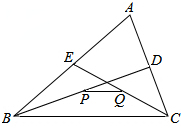

| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:6 |
9.已知$f(x)=\left\{\begin{array}{l}{|lg|x||\\;x≠0}\\{0\\;x=0}\end{array}\right.$,关于x的方程f2(x)+bf(x)+c=0有7个不同的解,则满足b,c的条件是( )
| A. | b<0,c<0 | B. | b<0,c=0 | C. | b>0,c=0 | D. | b>0,c<0 |
10.已知α∩β=l,a?α,b?β,且a,b是异面直线,那么直线l( )
| A. | 至多与a,b中的一条相交 | B. | 至少与a,b中的一条平行 | ||
| C. | 与a,b都相交 | D. | 至少与a,b中的一条相交 |
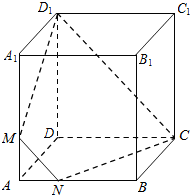 如图,已知正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上
如图,已知正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上