题目内容
已知函数f(x)=
答案:
解析:
解析:
| 解:∵f(2)=1,∴1= 又∵f(x)=x有惟一解,即 ∴x· 得x1=0,x2= 得b=1. ② 由①、②,得 ∴f(x)= 故f[f(-3)]=f( |

练习册系列答案
相关题目
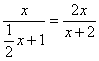
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有