题目内容
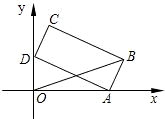 如图,矩形的长
如图,矩形的长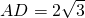 ,宽AB=1,A,D两点分别在x,y轴的正半轴上移动,B,C两点在第一象限.求OB2最大值.
,宽AB=1,A,D两点分别在x,y轴的正半轴上移动,B,C两点在第一象限.求OB2最大值.
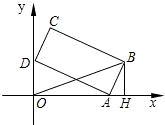 解:过点B作BH⊥OA,垂足为H.
解:过点B作BH⊥OA,垂足为H.设∠OAD=θ,则
 .
.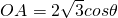 ,
,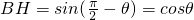 ,
,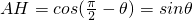 .
.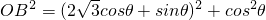
=
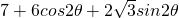 .
.=7+
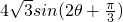
由
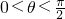 知
知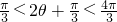 ,
,所以,当
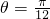 时,OB2取得最大值
时,OB2取得最大值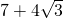 .
.分析:过点B作BH⊥OA,垂足为H.设∠OAD=θ进而表示出∠BAH和OA,HB,AH,然后利用勾股定理求得OB的解析式,利用θ的范围确定OB2最大值.
点评:本题主要考查了解三角形的实际应用.解题的关键是根据题意建立三角函数模型,借助三角函数的基本性质解决问题.

练习册系列答案
相关题目
 为迎接校庆,学校准备投入a元建造一个花圃(如图).已知矩形ABCD的造价为40元/m2,其余的两个半圆及两个圆的造价为20元/m2.两圆的直径分别为矩形的长和宽,由于矩形ABCD要种名贵花卉,故建造时要求矩形ABCD的面积越大越好.那么,当矩形ABCD的面积达到最大时,
为迎接校庆,学校准备投入a元建造一个花圃(如图).已知矩形ABCD的造价为40元/m2,其余的两个半圆及两个圆的造价为20元/m2.两圆的直径分别为矩形的长和宽,由于矩形ABCD要种名贵花卉,故建造时要求矩形ABCD的面积越大越好.那么,当矩形ABCD的面积达到最大时,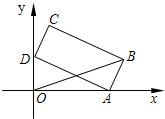 如图,矩形的长
如图,矩形的长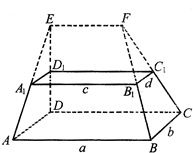 如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h.
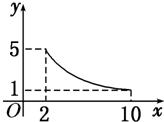
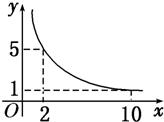
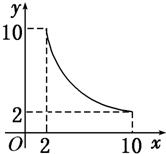
如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E,F两点,上、下底面矩形的长、宽分别为c,d与a,b,且a>c,b>d,两底面间的距离为h. 一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长、宽分别为x、y,剪去部分的面积为20,若2≤x≤10,记y=f(x),则y=f(x)的图象是( )
一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长、宽分别为x、y,剪去部分的面积为20,若2≤x≤10,记y=f(x),则y=f(x)的图象是( )