题目内容
用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?
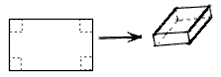
解:设容器的高为x,容器的体积为V,
则V=(90-2x)(48-2x)x(0<V<24)=4x3-276x2+4320x,
∴V′=12x2-552x+4320,
由V′=12x2-552x+4320=0得x1=10,x2=36,
∵x<10时,V′>0,10<x<36时,V′<0,x>36时,V′>0,
所以,当x=10时,V有极大值V(10)=1960,
又V(0)=0,V(24)=0,
所以当x=10时,V有最大值V(10)=1960。
则V=(90-2x)(48-2x)x(0<V<24)=4x3-276x2+4320x,
∴V′=12x2-552x+4320,
由V′=12x2-552x+4320=0得x1=10,x2=36,
∵x<10时,V′>0,10<x<36时,V′<0,x>36时,V′>0,
所以,当x=10时,V有极大值V(10)=1960,
又V(0)=0,V(24)=0,
所以当x=10时,V有最大值V(10)=1960。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 9、用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个大小相同的小正方形,然后把四边翻转90°角,再焊接而成(如图),当容器的容积最大时,该容器的高为( )
9、用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个大小相同的小正方形,然后把四边翻转90°角,再焊接而成(如图),当容器的容积最大时,该容器的高为( ) 21、用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?
21、用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?
