题目内容
一次演讲比赛中，需要安排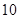
名选手的出场顺序，方法是按照姓氏笔画的多少（由少到多）安排，如姓氏笔画数相同，则顺序任意.统计发现，10名选手中姓氏笔画为4画的有2人，5画的有3人，6画的有4人，7画的有1人，则不同的出场顺序共有（ ）
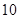名选手的出场顺序，方法是按照姓氏笔画的多少（由少到多）安排，如姓氏笔画数相同，则顺序任意.统计发现，10名选手中姓氏笔画为4画的有2人，5画的有3人，6画的有4人，7画的有1人，则不同的出场顺序共有（ ） | A．24种 | B．48种 | C．144种 | D．288种 |
D
本题中出场顺序方法种数的求解可以分为四步求解，先安排姓氏笔画为4画的选手，再安排五画的，第三步安排6画的，最后安排四画的，由乘法原理计算出结果，找出正确选项即可
解答：解：由题意，出场顺序方法种数的求解可以分为四步求解
因为10名选手中姓氏笔画为4画的有2人，5画的有3人，6画的有4人，7画的有1人，
故不同的出场顺序共有A22×A33×A44×1=288种
故选D
解答：解：由题意，出场顺序方法种数的求解可以分为四步求解
因为10名选手中姓氏笔画为4画的有2人，5画的有3人，6画的有4人，7画的有1人，
故不同的出场顺序共有A22×A33×A44×1=288种
故选D
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
少有一人参加，且
若甲、乙同时参加,则他们发言时顺序不能相邻，那么不同的发言顺序种类为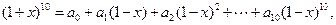
则
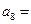
00米接力．如果第一棒只能从甲、乙、丙三人中产生，最后一棒只能从甲、乙两人中产生，则不同的安排棒次方案共有 种．（用数字作答）．