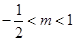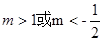题目内容
(本题满分14分)
已知函数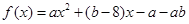 ,当
,当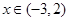 时,
时,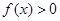 ;
;
当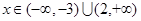 时,
时,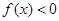 .
.
(1)求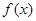 在
在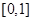 内的值域;
内的值域;
(2)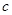 为何值时,
为何值时,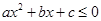 的解集为
的解集为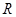 .
.
已知函数
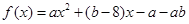 ,当
,当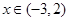 时,
时,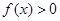 ;
;当
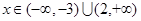 时,
时,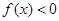 .
.(1)求
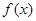 在
在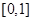 内的值域;
内的值域;(2)
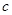 为何值时,
为何值时,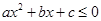 的解集为
的解集为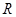 .
.(1)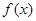 在
在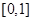 内的值域为
内的值域为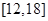 .
.
(2)当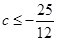 时,
时,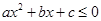 的解集为
的解集为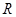 .
.
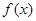 在
在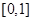 内的值域为
内的值域为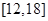 .
.(2)当
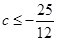 时,
时,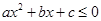 的解集为
的解集为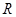 .
.试题分析:由题意可得当x=-3和x=2时,有y=0,代入可求a,b,进而可求f(x)
(1)由二次函数的性质可判断其在[0,1]上的单调性,进而可求函数的值域
(2)令g(x)=-3x2+5x+c,要使g(x)≤0的解集为R.则△≤0,解不等式可求
解:由题意可知
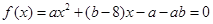 的两根分别为
的两根分别为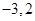 ,且
,且 ,则由韦达定理可得:
,则由韦达定理可得: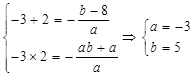 .
.故
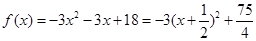 ,
,(1)
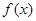 在
在 内单调递减,故
内单调递减,故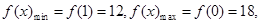
故
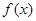 在
在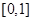 内的值域为
内的值域为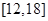 .
.(2)
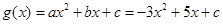 ,则要使
,则要使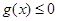 的解集为R,只需要方程
的解集为R,只需要方程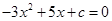 的判别式
的判别式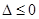 ,即
,即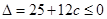 ,解得
,解得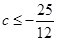 .
.∴当
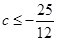 时,
时,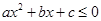 的解集为
的解集为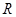 .
.点评:解决该试题的关键是对于二次函数单调性性质的运用,以及二次不等式的恒陈立问题的等价转化。

练习册系列答案
相关题目
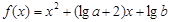 满足
满足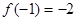 , 且对于任意
, 且对于任意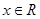 ,恒有
,恒有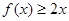 成立.(1)求实数
成立.(1)求实数 的值;
的值; 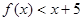 .
.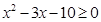 的解集是
的解集是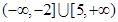
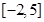
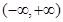
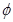
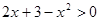 的解集是( )
的解集是( )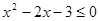 的解集是
的解集是 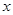 的不等式
的不等式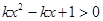 恒成立,则实数k的取值范围是__________________.
恒成立,则实数k的取值范围是__________________. ,[0.5]=0,则使[x2-1]=3的x的取值范围是
,[0.5]=0,则使[x2-1]=3的x的取值范围是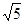 )
)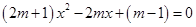 有一正根和一负根,则实数
有一正根和一负根,则实数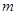 的取值范围( )
的取值范围( )