题目内容
若椭圆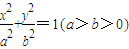
的离心率
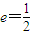，右焦点为F（c，0），方程ax2+2bx+c=0的两个实数根分别是x1和x2，则点P（x1，x2）到原点的距离为（ ）
A．
B．
C．2
D．
【答案】分析：利用一元二次方程根与系数的关系求出 x1 +x2 和x1 •x2 的值，再利用椭圆的简单性质求出P（x1，x2）到原点的距离．
解答：解：由题意知 x1 +x2 =-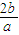
=-2 
，∴（x1+x2）2=4（1-e2）=3 ①，
x1 •x2 =
=
②，由①②解得 x12+x22=2，故P（x1，x2）到原点的距离为 
=
，
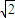故选 A．
点评：本题考查一元二次方程根与系数的关系，两点间的距离公式，椭圆的标准方程，以及椭圆的简单性质的应用．
解答：解：由题意知 x1 +x2 =-
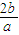=-2 ，∴（x1+x2）2=4（1-e2）=3 ①，x1 •x2 =
= ②，由①②解得 x12+x22=2，故P（x1，x2）到原点的距离为 =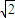，故选 A．
点评：本题考查一元二次方程根与系数的关系，两点间的距离公式，椭圆的标准方程，以及椭圆的简单性质的应用．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
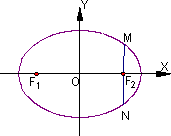
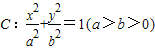的离心率e＝
，
的离心率e=
，左右两个焦分别为F1，F2．过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点，且|MN|=2．