题目内容
(本题共12分)
已知函数 ,其中
,其中 且
且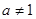 。
。
(Ⅰ)讨论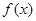 的单调性;
的单调性;
(Ⅱ)求函数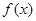 在〔
在〔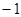 ,
,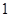 〕上的最小值和最大值。
〕上的最小值和最大值。
【答案】
解:(Ⅰ)函数 在
在 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。
(Ⅱ)当 时,
时, 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为 ;
;
当 时,
时, 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为 。
。
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)主要是对于 ,∴
,∴ ,参数a分类讨论得到函数的单调区间。
,参数a分类讨论得到函数的单调区间。
(2)由(Ⅰ)知 在
在 单调递减,在
单调递减,在 在单调递增
在单调递增
 当
当 时,
时, 取得最小值
取得最小值
 ,然后比较大小,构造函数来完成得到结论。
,然后比较大小,构造函数来完成得到结论。
解:(Ⅰ)  ,∴
,∴ 。
。
① 当 时,
时, ,由
,由 可得
可得 ;由
;由 可得
可得
 在
在 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。
②当 时,
时, ,由
,由 可得
可得 ;由
;由 可得
可得
 在
在 上单调递减,在
上单调递减,在 上单调递增。
上单调递增。
综上可得,函数 在
在 上单调递减,在
上单调递减,在 上单调递增。………4分
上单调递增。………4分
(Ⅱ)由(Ⅰ)知 在
在 单调递减,在
单调递减,在 在单调递增
在单调递增
 当
当 时,
时, 取得最小值
取得最小值
 ……………………………………………………6分
……………………………………………………6分
 ,
,
设  ,则
,则 。
。
∵ (当且仅当
(当且仅当 时
时 )∴
)∴ 在
在 上单调递增.
上单调递增.
又∵ ,
,
∴①当 时,
时, ,即
,即 ,
,
这时, 在
在 上的最大值为
上的最大值为 ;
;
②当 时,
时,  ,即
,即
这时, 在
在 上的最大值为
上的最大值为 。
。
综上,当 时,
时, 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为 ;
;
当 时,
时, 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为 …………12分
…………12分

练习册系列答案
相关题目
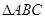 的三个内角且向量
的三个内角且向量 共线。
共线。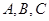 的对边分别是
的对边分别是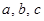 ,且满足
,且满足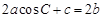 ,试判断
,试判断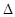
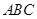 的形状.
的形状.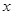 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为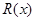 万元,且
万元,且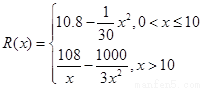 .
.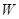 (万元)关于年产量
(万元)关于年产量 ,其中
,其中 且
且 。
。
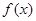 的单调性;
的单调性; ,
, 〕上的最小值和最大值。
〕上的最小值和最大值。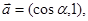
 ,
, ,且
,且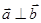
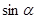 的值 (2)求
的值 (2)求