题目内容
已知直线 与曲线
与曲线 恰有两个不同的交点,记k的所有可能取值构成集合A;P(x,y)是椭圆
恰有两个不同的交点,记k的所有可能取值构成集合A;P(x,y)是椭圆 上一动点,
上一动点, 与点P关于直线y=x+1对称,记
与点P关于直线y=x+1对称,记 的所有可能取值构成集合B,若随机的从集合A,B中分别抽出一个元素
的所有可能取值构成集合B,若随机的从集合A,B中分别抽出一个元素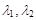 ,则
,则 的概率是___________
的概率是___________

解析试题分析:由 ,当x≥0时,显然k>0,两边平方得
,当x≥0时,显然k>0,两边平方得 ,即
,即
由题意,该方程有两个不相等的正实数根
即 即
即 结合k>0解得k∈(0,1),即A=(0,1)
结合k>0解得k∈(0,1),即A=(0,1)
对于椭圆 ,由于原点关于y=x+1的对称点为(-1,1)
,由于原点关于y=x+1的对称点为(-1,1)
所以,椭圆关于y=x+1的对称椭圆为 ,
, 在改椭圆上,可知y1-1∈[-4,4]
在改椭圆上,可知y1-1∈[-4,4]
于是 ∈[-1,1],即B=[-1,1]
∈[-1,1],即B=[-1,1]
【方法一】由 ,分别以
,分别以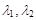 为横坐标和纵坐标,
为横坐标和纵坐标,
可知点(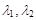 )构成一个面积为2的矩形
)构成一个面积为2的矩形
其中满足 的是图中阴影部分,面积为
的是图中阴影部分,面积为
所以,满足 的概率是
的概率是

【方法二】当 时,此事件发生的概率为
时,此事件发生的概率为 ,此时必有
,此时必有
当 时,此事件发生的概率为
时,此事件发生的概率为 ,此时
,此时 与
与 概率相等,各占
概率相等,各占 ,于是此时满足
,于是此时满足 的概率为
的概率为 .
.
以上两事件互斥,且[-1,0]与(0,1]的区间长度相等,故满足 的概率为
的概率为 .
.
考点:直线与曲线的交点,轴对称图形,坐标的取值范围,几何概型.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
从含有4个元素的集合的所有子集中任取一个,所取的子集是含有2个元素的集合的概率是( )
A. | B. | C. | D. |
在区间 上随机取一个数
上随机取一个数 ,
, 的值介于0到
的值介于0到 之间的概率为
之间的概率为
A. | B. | C. | D. |
 内随机地取出一个数
内随机地取出一个数 ,使得
,使得 的概率为 .
的概率为 .
 ,
, ,点P的坐标为(
,点P的坐标为( ,
, ),
), ,
, ,则点P在直线
,则点P在直线 下方的概率为 .[
下方的概率为 .[  的概率是频率的稳定值,频率是概率的近似值;②一次试验中不同的基本事件不可能同时发生;③任意事件
的概率是频率的稳定值,频率是概率的近似值;②一次试验中不同的基本事件不可能同时发生;③任意事件 总满足
总满足 ;其中正确的是 ;(写出所有正确说法的序号)
;其中正确的是 ;(写出所有正确说法的序号) 分别在抛物线
分别在抛物线 和
和 上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在阴影区域的概率是 .
上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在阴影区域的概率是 .
 .据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.
.据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.