题目内容
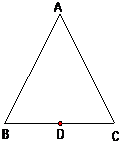 如图所示,D为正△ABC的边BC的中点,从D发出光线射到AC边每一点的概率相同,求由D发出的光线,先后经AC边,AB边反射后仍落在BC边上的概率.
如图所示,D为正△ABC的边BC的中点,从D发出光线射到AC边每一点的概率相同,求由D发出的光线,先后经AC边,AB边反射后仍落在BC边上的概率.分析:利用光的反射定律及等边三角形的性质证明△DD1C∽△D2D1A∽△D2D3B,再根据相似三角形对应边成比例得到用含D3B的代数式表示D1C的式子,然后由0<BD3<2 即可求出D1C长的取值范围,然后代入几何概率的求解公式可求
解答: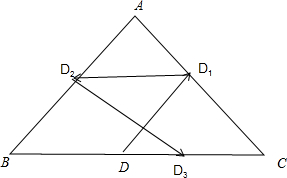 解:设正三角形的边长为2
解:设正三角形的边长为2
∵反射角等于入射角,
∴∠DD1C=∠D2D1A=∠D2D3B,
又∵∠C=∠A=∠B=60°,
∴△DD1C∽△D2D1A∽△D2D3B,
∴
=
=
设D1C=x,D2A=y,则D1A=2-x,D2B=2-y.
∴
=
=
∴
∴x=
(2+D3B).
又∵0<BD3<2,
∴
<x<
所求的概率P=
=
 解:设正三角形的边长为2
解:设正三角形的边长为2∵反射角等于入射角,
∴∠DD1C=∠D2D1A=∠D2D3B,
又∵∠C=∠A=∠B=60°,
∴△DD1C∽△D2D1A∽△D2D3B,
∴
| CD |
| CD1 |
| AD2 |
| AD1 |
| BD2 |
| BD3 |
设D1C=x,D2A=y,则D1A=2-x,D2B=2-y.
∴
| 1 |
| x |
| y |
| 2-x |
| 2-y |
| BD3 |
∴
|
∴x=
| 1 |
| 3 |
又∵0<BD3<2,
∴
| 2 |
| 3 |
| 4 |
| 3 |
所求的概率P=
| ||||
| 2 |
| 1 |
| 3 |
点评:本题主要考查了等边三角形的性质,在解题时要根据等边三角形的性质找出对应点是解此题的关键,难度较大.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
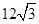 的正三棱柱的三视图,如图所示,则此正三棱柱的侧视图面积为( )
的正三棱柱的三视图,如图所示,则此正三棱柱的侧视图面积为( )

 B.
B.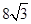 C.
C.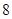 D.
D.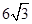

 B、
B、
 D、
D、
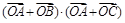 =
=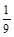 (B)
(B) 
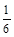 (D)
(D) 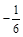

 ,底面边长为
,底面边长为 ,E是SA的中点,则异面直线BE与SC所成角的大小为
( )
,E是SA的中点,则异面直线BE与SC所成角的大小为
( )
 B.
B. C.
C. D.
D.
