题目内容
.用5种不同的颜色给图中所给出的四个区域涂色，每个区域涂一种颜色，若要求相邻（有公共边）的区域不同色，那么共有多少种不同的涂色方法？
260
完成该件事可分步进行.
涂区域1，有5种颜色可选.
涂区域2，有4种颜色可选.
涂区域3，可先分类：若区域3的颜色与2相同，则区域4有4种颜色可选.若区域3的颜色与2不同，则区域3有3种颜色可选，此时区域4有3种颜色可选.
所以共有5×4×（1×4+3×3）=260种涂色方法.
涂区域1，有5种颜色可选.
涂区域2，有4种颜色可选.
涂区域3，可先分类：若区域3的颜色与2相同，则区域4有4种颜色可选.若区域3的颜色与2不同，则区域3有3种颜色可选，此时区域4有3种颜色可选.
所以共有5×4×（1×4+3×3）=260种涂色方法.
练习册系列答案
相关题目
,
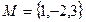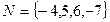从两个集合中各取一个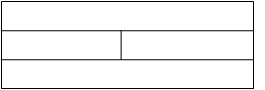
放方案有