题目内容
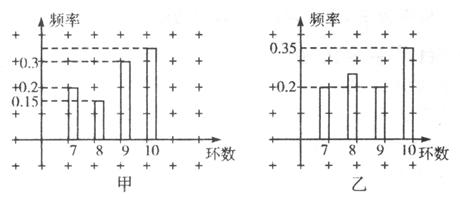
甲、乙两射击运动员进行射击比赛,射击次数相同,已知两运动员击中的环数ξ稳定在7,8,9,10环,他们比赛成绩的频率分布条形图如下:(如果将频率近似的看作概率)(I)估计乙运动员击中8环的概率,并求甲、乙同时击中9环以上(包括9环)的概率.
(II)求甲运动员击中环数ξ的概率分布列及期望;若从甲、乙运动员中只能挑选一名参加某大型比赛,你认为让谁参加比较合适?


【答案】分析:(Ⅰ)记“甲运动员击中i环”为事件Ai;“乙运动员击中i环”为事件Bi(i=1,2,3,…,10),P(B8)=1-P(B7)-P(B9)-P(B10)=0.25.P(A9)+P(A10)=0.65,P(B9)+P(B10)=0.55,由此能求出甲、乙同时击中9环以上(包括9环)的概率.
(Ⅱ)ξ的可能取值:7、8、9、10.分别求出甲运动员射击环数ξ的概率分布列、期望而却步和乙运动员射击环数ξ的概率分布列、期望可知选甲去比较合适.
解答:解:(Ⅰ)记“甲运动员击中i环”为事件Ai;“乙运动员击中i环”为事件Bi(i=1,2,3,…,10)
∴P(B8)=1-P(B7)-P(B9)-P(B10)=1-0.2-0.2-0.35=0.25.(2分)
∵P(A9)+P(A10)=1-0.15-0.2=0.65,P(B9)+P(B10)=0.2+0.35=0.55,
∴甲、乙同时击中9环以上(包括9环)的概率:0.65×0.55=0.3575.(6分)
(Ⅱ)ξ的可能取值:7、8、9、10.
甲运动员射击环数ξ的概率分布列为:
甲运动员射击环数ξ的期望E1ξ=7×0.2+8×0.15+9×0.3+10×0.35=8.8.(9分)
乙运动员射击环数ξ的概率分布列为:
乙运动员射击环数ξ的期望E2ξ=7×0.2+8×0.15+9×0.2+10×0.35=7.9
从以上分析可知选甲去比较合适(12分)
点评:本题考查离散型随机变量的分布列和期望,解题时要认真审题,仔细解答,注意概率计算公式的合理运用.
(Ⅱ)ξ的可能取值:7、8、9、10.分别求出甲运动员射击环数ξ的概率分布列、期望而却步和乙运动员射击环数ξ的概率分布列、期望可知选甲去比较合适.
解答:解:(Ⅰ)记“甲运动员击中i环”为事件Ai;“乙运动员击中i环”为事件Bi(i=1,2,3,…,10)
∴P(B8)=1-P(B7)-P(B9)-P(B10)=1-0.2-0.2-0.35=0.25.(2分)
∵P(A9)+P(A10)=1-0.15-0.2=0.65,P(B9)+P(B10)=0.2+0.35=0.55,
∴甲、乙同时击中9环以上(包括9环)的概率:0.65×0.55=0.3575.(6分)
(Ⅱ)ξ的可能取值:7、8、9、10.
甲运动员射击环数ξ的概率分布列为:
| ξ | 7 | 8 | 9 | 10 |
| P | 0.2 | 0.15 | 0.3 | 0.35 |
乙运动员射击环数ξ的概率分布列为:
| ξ | 7 | 8 | 9 | 10 |
| P | 0.2 | 0.15 | 0.2 | 0.35 |
从以上分析可知选甲去比较合适(12分)
点评:本题考查离散型随机变量的分布列和期望,解题时要认真审题,仔细解答,注意概率计算公式的合理运用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 19、
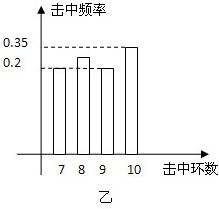
19、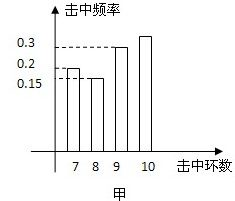 甲、乙两射击运动员进行射击比赛,射击次数相同,已知两运动员击中的环数ξ稳定在7,8,9,10环,他们比赛成绩的频率分布条形图如下:(如果将频率近似的看作概率)
甲、乙两射击运动员进行射击比赛,射击次数相同,已知两运动员击中的环数ξ稳定在7,8,9,10环,他们比赛成绩的频率分布条形图如下:(如果将频率近似的看作概率)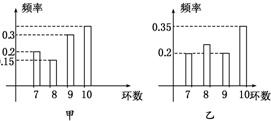 5、甲、乙两射击运动员进行比赛,射击相同的次数,已知两运动员射击的环数稳定在7,8,9,10环,他们的成绩频率分布条形图如图:由乙击中8环及甲击中10环的概率与甲击中环数的平均值都正确的一组数据依次是
5、甲、乙两射击运动员进行比赛,射击相同的次数,已知两运动员射击的环数稳定在7,8,9,10环,他们的成绩频率分布条形图如图:由乙击中8环及甲击中10环的概率与甲击中环数的平均值都正确的一组数据依次是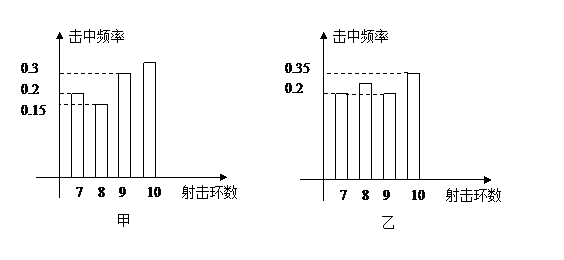
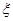 稳定在7,8,
稳定在7,8,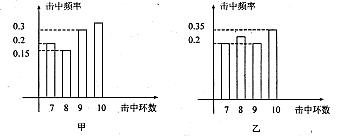 [来源:学|科|网Z|X|X|K]
[来源:学|科|网Z|X|X|K]