题目内容
在各项都为正数的等比数列{an}中,公比q=2,前三项和为21,则a3+a4+a5=( ).
| A.33 | B.72 | C.84 | D.189 |
C
解析试题分析:根据等比数列{an}中,首项a1=3,前三项和为21,可求得q,根据等比数列的通项公式,分别求得a3,a4和a5代入a3+a4+a5,即可得到答案.解:在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,故3+3q+3q2=21,∴q=2,∴a3+a4+a5=21×22=84,故选C
考点:等比数列的性质
点评:本题主要考查了等比数列的性质.要理解和记忆好等比数列的通项公式,并能熟练灵活的应用

练习册系列答案
相关题目
在等比数列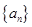 中, 若
中, 若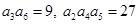 , 则
, 则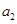 的值为( )
的值为( )
A. | B. | C.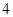 | D. |
已知等比数列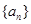 中,公比
中,公比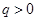 ,若
,若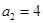 ,则
,则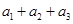 的最值情况为
的最值情况为
A.有最小值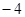 | B.有最大值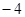 |
C.有最小值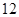 | D.有最大值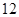 |
已知数列 满足
满足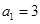 ,
,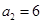 ,
,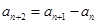 ,则
,则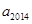 =( )
=( )
| A.6 | B.-3 | C.-6 | D.3 |
等比数列 的前
的前 项和为
项和为 ,若
,若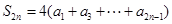 ,
,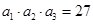 ,则
,则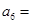 ( )
( )
A. | B. | C.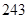 | D.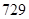 |
等比数列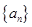 的前
的前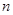 项和为
项和为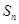 ,若
,若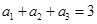 ,
,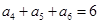 ,则
,则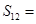 ( )
( )
| A.15 | B.30 | C.45 | D.60 |
已知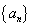 是首项为1的等比数列,
是首项为1的等比数列, 是
是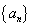 的前n项和,且
的前n项和,且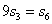 ,则数列
,则数列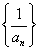 的前5项和为
的前5项和为
A.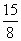 或5 或5 | B.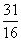 或5 或5 | C.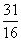 | D.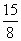 |
设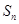 是等比数列
是等比数列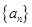 的前n项和,
的前n项和,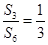 ,则
,则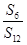 等于( )
等于( )
A.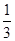 | B. | C.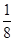 | D.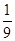 |
 满足:
满足: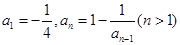 ,则
,则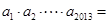 .
.