题目内容
当a取不同的实数时,直线(a-1)x-y+2a+1=0恒过一个定点,这个定点的坐标是________.
(-2,3)
分析:直线方程即 a(x+2)+(-x-y+1)=0,一定经过x+2=0和-x-y+1=0 的交点,联立方程组可求定点的坐标.
解答:证明:直线(a-1)x-y+2a+1=0 即 a(x+2)+(-x-y+1)=0,
根据a的任意性可得 ,解得
,解得 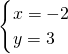 ,
,
∴当a取不同的实数时,直线(a-1)x-y+2a+1=0恒过一个定点,这个定点的坐标是(-2,3).
故答案为:(-2,3).
点评:本题考查经过两直线交点的直线系方程形式,直线 k(ax+by+c)+(mx+ny+p)=0 表示过ax+by+c=0和mx+ny+p=0的交点的一组相交直线,但不包括ax+by+c=0这一条.
分析:直线方程即 a(x+2)+(-x-y+1)=0,一定经过x+2=0和-x-y+1=0 的交点,联立方程组可求定点的坐标.
解答:证明:直线(a-1)x-y+2a+1=0 即 a(x+2)+(-x-y+1)=0,
根据a的任意性可得
 ,解得
,解得 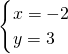 ,
,∴当a取不同的实数时,直线(a-1)x-y+2a+1=0恒过一个定点,这个定点的坐标是(-2,3).
故答案为:(-2,3).
点评:本题考查经过两直线交点的直线系方程形式,直线 k(ax+by+c)+(mx+ny+p)=0 表示过ax+by+c=0和mx+ny+p=0的交点的一组相交直线,但不包括ax+by+c=0这一条.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
当
a取不同的实数时,方程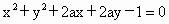 所表示的圆的圆心
所表示的圆的圆心
[
]|
A .都在直线y=x上 |
B .都在直线y=-x上 |
|
C .都在直线y=x,或y=-x上 |
D .不在直线上 |
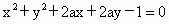 可以得到不同的圆,则
可以得到不同的圆,则
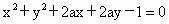 所表示的圆的圆心
所表示的圆的圆心