题目内容
若三角形内切圆的半径为r,三边长为 ,则三角形的面积
,则三角形的面积 ,根据类比思想,若四面体内切球半径为R,四个面的面积为S1、S2、S3、S4,则四面体的体积V= .
,根据类比思想,若四面体内切球半径为R,四个面的面积为S1、S2、S3、S4,则四面体的体积V= .
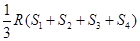
解析试题分析:设四面体的内切球的球心为O,则球心O到四个面的距离都是R,所以四面体的体积等于以O为顶点,分别以四个面为底面的4个三棱锥体积的和.故答案为: R(S1+S2+S3+S4).
R(S1+S2+S3+S4).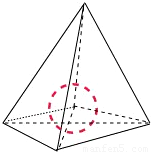
考点:类比推理.

练习册系列答案
相关题目
用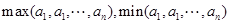 分别表示
分别表示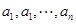 中的最大与最小者,有下列结论:
中的最大与最小者,有下列结论:
①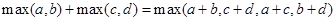 ;
;
②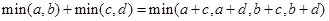 ;
;
③若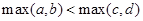 ,则
,则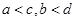 ;
;
④若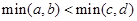 ,则
,则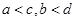 。
。
其中正确结论的个数是( )
| A.0 | B.1 | C.2 | D.3 |
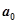 ,用
,用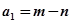 ,然后继续对
,然后继续对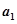 重复上述变换,得数
重复上述变换,得数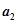 ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论 的周长为
的周长为 ,面积为
,面积为 ,则
,则 .将此结论类比到空间,已知四面体
.将此结论类比到空间,已知四面体 的表面积为
的表面积为 ,则四面体
,则四面体 .
.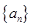 的首项为
的首项为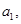 公差为
公差为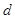 ,前
,前 项的和为
项的和为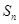 ,则数列
,则数列 为等差数列,且通项为
为等差数列,且通项为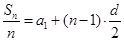 .类似地,请完成下列命题:若各项均为正数的等比数列
.类似地,请完成下列命题:若各项均为正数的等比数列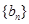 的首项为
的首项为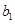 ,公比为
,公比为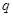 ,前
,前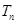 ,则 .
,则 . ,经计算得
,经计算得 ,
, ,
,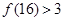 ,
,
 ,观察上述结果,可归纳出的一般结论为 .
,观察上述结果,可归纳出的一般结论为 . 中,不等式
中,不等式 成立;在凸四边形ABCD中,
成立;在凸四边形ABCD中,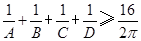 成立;在凸五边形ABCDE中,不等式
成立;在凸五边形ABCDE中,不等式 成立,…,依此类推,在凸n边形
成立,…,依此类推,在凸n边形 中,不等式
中,不等式 _____成立.
_____成立. 个等式为 .
个等式为 .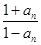 (n∈N*),则a3=________,a1·a2·a3·…·a2007=________.
(n∈N*),则a3=________,a1·a2·a3·…·a2007=________.