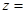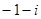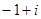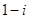题目内容
若z∈C,且|z+2-2i|=1,则|z-2-2i|的最小值与最大值分别是( )
| A.2 ,3 | B.3 ,5 | C.4 ,6 | D.4,5 |
B
解析试题分析:因为|z+2-2i|=1表示半径为1,圆心为A(-2,2)的圆,所以|z-2-2i|表示圆上的点到B(2,2)距离。结合图形分析知,其最大值为|AB|+1=5,最小值为|AB|-1=3,故选B。
考点:本题主要考查复数模的概念及其几何意义。
点评:中档题,利用数形结合思想,明确|z+2-2i|=1表示圆,从而转化成圆上的点到(2,2)距离的最值问题。

练习册系列答案
相关题目
复数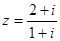 的共轭复数为
的共轭复数为
A.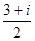 | B.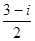 | C.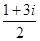 | D.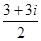 |
复数z=i+i2+i3+i4的值是 ( )
| A.-1 | B.0 | C.1 | D.i |
设a∈R,i是虚数单位,则当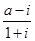 是纯虚数时,实数a为
是纯虚数时,实数a为
A.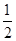 | B.- 1 | C.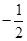 | D.1 |
i(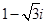 )=( )
)=( )
A.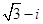 | B.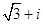 | C. | D. |
设复数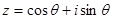 ,
,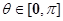 ,
,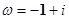 ,则
,则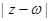 的最大值是( )
的最大值是( )
A.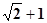 | B.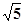 | C.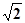 | D.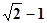 |
已知复数 在复平面上对应点为
在复平面上对应点为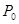 ,则
,则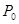 关于直线
关于直线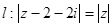 的对称点的复数表示是( ).
的对称点的复数表示是( ).
A.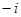 | B.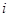 | C.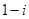 | D.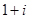 |
设复数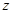 满足
满足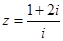 (
(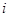 为虚数单位),则复数
为虚数单位),则复数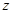 在复平面内对应的点位于
在复平面内对应的点位于
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
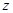 是复数,i是虚数单位,
是复数,i是虚数单位,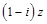 在复平面中对应的点为P,若P对应的复数是模等于2的负实数,那么
在复平面中对应的点为P,若P对应的复数是模等于2的负实数,那么