题目内容
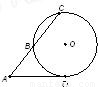 如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=2
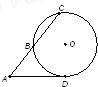
如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=2 ,AC=6,圆O的半径为3,则圆心O到AC的距离为 .
,AC=6,圆O的半径为3,则圆心O到AC的距离为 .
【答案】分析:要求圆心O到AC的距离,我们要先做出O点到AC的垂线段OE,则OE的长度即为所求,根据半径、半弦长(BE)、弦心距(OE)构成直角三角形,满足勾股定理,故我们要要求出半弦长(BE),根据切割线定理,我可以求出AB长,进而得到BE,代入即可得到答案.
解答: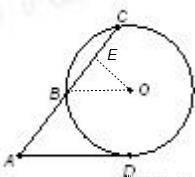 解:连接OB,过O点向AC引垂线,垂足为E,
解:连接OB,过O点向AC引垂线,垂足为E,
∵AD=2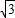 ,AC=6,由切割线定理可得,
,AC=6,由切割线定理可得,
AD2=AC•AB,∴AB=2,
∴BC=4,
由垂径定理得BE=2.
又∵R=OB=3,
∴OE=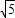 ,
,
故答案为: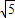 .
.
点评:要求圆到割线的距离,即弦心距,我们最常用的性质是:半径、半弦长(BE)、弦心距(OE)构成直角三角形,满足勾股定理,求出半径和半弦长,代入即可求解.
解答:
 解:连接OB,过O点向AC引垂线,垂足为E,
解:连接OB,过O点向AC引垂线,垂足为E,∵AD=2
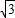 ,AC=6,由切割线定理可得,
,AC=6,由切割线定理可得,AD2=AC•AB,∴AB=2,
∴BC=4,
由垂径定理得BE=2.
又∵R=OB=3,
∴OE=
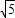 ,
,故答案为:
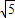 .
.点评:要求圆到割线的距离,即弦心距,我们最常用的性质是:半径、半弦长(BE)、弦心距(OE)构成直角三角形,满足勾股定理,求出半径和半弦长,代入即可求解.

练习册系列答案
相关题目
 如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=2
如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=2
 (几何证明选讲选做题)如图,从圆O外一点A引圆的切线AD和割线ABC,已知AC=6,圆O的半径为3,圆心O到AC的距离为
(几何证明选讲选做题)如图,从圆O外一点A引圆的切线AD和割线ABC,已知AC=6,圆O的半径为3,圆心O到AC的距离为 (2007•汕头二模)如图,从圆O外一点A引切线AD和割线ABC,AB=3,BC=2,则切线AD的长为
(2007•汕头二模)如图,从圆O外一点A引切线AD和割线ABC,AB=3,BC=2,则切线AD的长为 (考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分)
(考生注意:只能从下列A、B、C三题中选做一题,如果多做,则按第一题评阅记分)