题目内容
设y=f（x）是R上的减函数，则y=f（|x-3|）的单调递减区间为 ．
分析：取一个特殊的f（x）作出其图象，则有f（x）的图象与函数y=f（|x-3|）的图象关系，作出y=f（|x-3|）的图象求解
解答：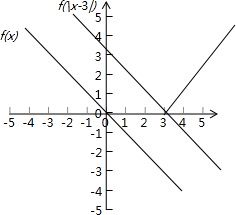
解：如图所示：
函数y=f（|x-3|）的单调递减区间是[3，+∞），
故答案为：[3，+∞）
解：如图所示：函数y=f（|x-3|）的单调递减区间是[3，+∞），
故答案为：[3，+∞）
点评：本题主要考查数形结合法求函数单调区间问题．
练习册系列答案
相关题目