题目内容

设A，B，C，D是空间不共面的四点，且满足
AB
•
AC
=0，
AC
•
AD
=0，
AB
•
AD
=0，则△BCD是
 
三角形
分析：由题意知，AB⊥AC，AC⊥AD，AB⊥AD，设 AB=a，AC=b，AD=c，由勾股定理可求BC、CD、BD的长度，△BCD中，有余弦定理得B，C，D三个角的余弦值都是正数，故B，C，D都是锐角．
解答：解：∵
AB
•
AC
=0，
AC
•
AD
=0，
AB
•
AD
=0，
∴AB⊥AC，AC⊥AD，AB⊥AD，
设 AB=a，AC=b，AD=c，则BC=
a2+b2
，CD=
b2+c2
，BD=
c2+a2
，
△BCD中，有余弦定理得cosB=
a2
a2+b2
•
a2+c2
＞0，
同理可证，cosC＞0，cosD＞0，
∴B，C，D都是锐角，
∴△BCD是锐角三角形，
故答案为 锐角．
点评：本题考查平面向量数量积的运算，三角形中的勾股定理和余弦定理的应用．
练习册系列答案
相关题目
7、设A={x|x=2k，k∈Z}，B={x|x=2k+1，k∈Z}，C={x|x=2（k+1），k∈Z}，D={x|x=2k-1，k∈Z}，在A、B、C、D中，哪些集合相等，哪些集合的交集是空集？
（2013•长春一模）对于非空实数集A，记A*={y|?x∈A，y≥x}．设非空实数集合M、P满足：M⊆P，且若x＞1，则x∉P．现给出以下命题：
①对于任意给定符合题设条件的集合M、P，必有P*⊆M*；
②对于任意给定符合题设条件的集合M、P，必有M*∩P≠∅；
③对于任意给定符合题设条件的集合M、P，必有M∩P*=∅；
④对于任意给定符合题设条件的集合M、P，必存在常数a，使得对任意的b∈M*，恒有a+b∈P*，
其中正确的命题是（　　）
设P、Q为两个非空实数集合，定义集合P+Q={a+b|a∈P,b∈Q},若P={0,2,5},Q={1,2,6}，则P+Q中元素的个数是(    )

A.9               B.8            C.7             D.6

设全集为U，若M.N都是U的非空子集，且，则有（     ）

A、          B、

C、      D、

 

设是两个非空实数集合，定义集合.

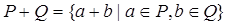若，则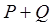中元素的个数是( 　)

A.  9       B. 8      C. 7      D.  6

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网