题目内容
若α是锐角,且 的值是 。
的值是 。
 的值是 。
的值是 。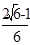
本试题主要是考查了三角函数中两角差的正弦公式的运用,以及运用凑角的思想求解函数值。
因为α是锐角,且
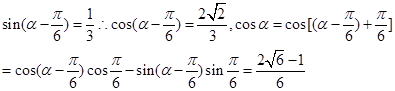
故答案为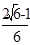
解决该试题的关键是将所求的表示为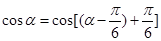 ,整体的思想来解决函数值。
,整体的思想来解决函数值。
因为α是锐角,且
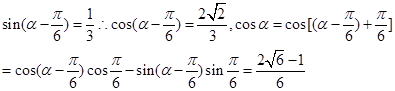
故答案为
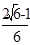
解决该试题的关键是将所求的表示为
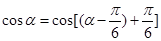 ,整体的思想来解决函数值。
,整体的思想来解决函数值。
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
题目内容
 的值是 。
的值是 。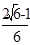
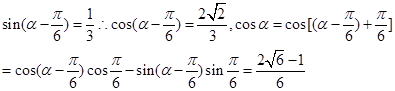
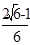
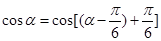 ,整体的思想来解决函数值。
,整体的思想来解决函数值。
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案