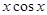题目内容
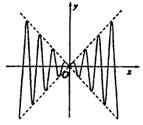
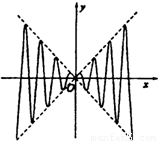
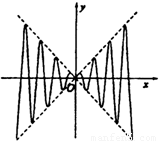
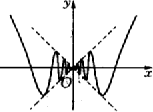
如图，虚线部分是四个象限的角平分线，实线部分是函数y=f（x）的部分图象，则f（x）可能是（ ）分析：由函数的图象可知y=f（x）为偶函数，可排除B，D，y=f（x）不经过（2π，4π2），可排除A，从而可得答案．
解答：解：由函数的图象可知y=f（x）为偶函数，
对于B，f（x）=xcosx为奇函数，可排除B；
同理，D中f（x）=x2sinx为奇函数，可排除D；
对于A，f（x）=x2cosx虽然为偶函数，但其曲线上的点（2π，4π2）在直线y=x的右上方，即不在图中的函数曲线上，故可排除A．
故选C．
对于B，f（x）=xcosx为奇函数，可排除B；
同理，D中f（x）=x2sinx为奇函数，可排除D；
对于A，f（x）=x2cosx虽然为偶函数，但其曲线上的点（2π，4π2）在直线y=x的右上方，即不在图中的函数曲线上，故可排除A．
故选C．
点评：本体考查函数的图象，着重考查函数的奇偶性的应用，突出排除法的应用，属于中档题．
练习册系列答案
相关题目
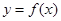的部分图象，则
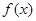可能是( )
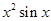B. 
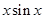
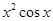D. 
